Нахождение суммы, произведения элементов массива

В Matlab для этого существуют следующие функции:

Функция sx=sum(X) в случае одномерного массива возвращает сумму элементов массива; в случае двумерного массива – это вектор-строка, содержащая суммы элементов каждого столбца;

Функция sx = sum(X, dim) возвращает вектор-строку, содержащую суммы элементов по столбцам вдоль размерности dim;

Функции csx=cumsum(X), csx=cumsum(X, dim), кроме того, возвращают все промежуточные результаты суммирования.

Функция px=prod(X) в случае одномерного массива возвращает произведение элементов массива; в случае двумерного массива – это вектор-строка, содержащая произведения элементов каждого столбца;

Функция px = prod(X, dim) возвращает вектор-строку, содержащую произведение элементов по столбцам вдоль размерности dim;

Функции cpx=cumprod(X), cpx=cumprod (X, dim), кроме того, возвращают все промежуточные результатыумножения.

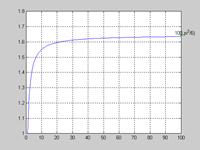
Пример: Найти частичную сумму ряда при заданном n (n=100). Сравнить численно полученный результат с точным 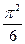. Построить график и график погрешности.

>> n=100;

>> k=1:n;

>> a=k.^-2;

>> s=cumsum(a);

>> l=pi^2/6

l = 1.6449

>> s(end)

ans = 1.6350

>> plot(n,cumsum(Un),100,l,'*')

>> grid on

>> xlabel('n');

>> ylabel('\sigma_{k=1}^n{1}/{k^2}');

>> relerr=abs(s-l)/l;

>> figure

>> semilogy(k,relerr);

>> xlabel('n');

>> ylabel('Relative error');

>> grid;

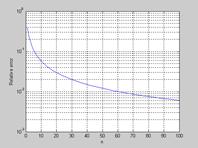
Сходимость не всегда столь очевидна как на этом графике.

Пример: Установить сходимость ряда 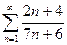, пользуясь графиком суммы ряда.

>> n=1:1000;

>> Un=(2.*n+4)./(7.*n+6);

>> cumsum(Un);

>> plot (cumsum(Un))

Из графика видно, что линия суммы уходит круто вверх и нельзя указать точку к которой стремиться эта линия, следовательно по определению ряд расходится.

Пример: Оценить сумму ряда с точностью до 10^-6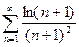

U1=log(2)/4;; % создаём файл-функцию и сохраняем под именем limit

s=U1;

n=1;

while abs(Un)>1e-6

Un=log(n+1)./(n+1).^2;

s=s+Un;

n=n+1;

end

disp('Число слагаемых')

disp(n-1)

disp('оценка суммы')

disp(s)

limit12 % в командной строке набираем имя файл-функции

Число слагаемых 2818

оценка суммы 1.93437594902582

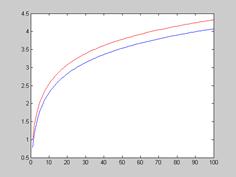
Пример: Исследовать на сходимость ряд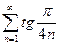

>> limit(tan(pi/(4*n)),n,inf)

ans = 0 % необходимый признак выполняется.

> n=100;

>> k=1:n;

>> a=tan(pi./(4.*k));

>> b=pi./(4.*k);

>> hold on;S1=cumsum(a);plot(S1,'r')

>> hold on;S2=cumsum(b);plot(S2,'b' )

Пример: Исследовать на сходимость ряд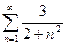

Исселуем по предельному признаку сравнения.

>> syms n; Un=3/(2+n^2); limit(Un,n,inf)

ans = 0 % необходимый признак выполняется- дополнительные исследования

>> Vn=1/n^2; % ряд сравнения обобщенно гармонический расходящийся

>>limit(Un/Vn,n,inf)

ans = 3 % ряд 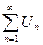расходится

Пример: Исследовать сходимость числовой ряд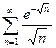

Исследуем по интегральному признаку Коши

int(exp(-sqrt(x))/sqrt(x),x,1,inf)

ans = 2*exp(-1) % интеграл сходится и ряд сходится

Пример: Исследовать сходимость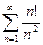

Исследуем по признаку Даламбера

>> syms n;Un=3^n/sym('n!');Un1=subs(Un,n,n+1)

Un1 =3^(n+1)/(n+1)!

>> limit(Un1/Un,n,inf)

ans = 0 % <1 – ряд сходится

Пример: Исследовать сходимость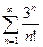

Исследуем по признаку Даламбера

>> syms n;Un=sym('n!')/n^2;Un1=subs(Un,n,n+1)

Un1 = (n+1)!/(n+1)^2

>> limit(Un1/Un,n,inf)

ans = inf % >1 – ряд расходится

Для записи факториала в символьном выражении можно использовать sym('n!') или 'n!'.

Пример: Исследовать сходимость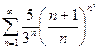

Исследуем по радикальному признаку Коши

>> syms n

>> limit((5/3^n*((n+1)/n)^n^2)^(1/n),n,inf)

ans = 1/3 % <1 – ряд сходится

Нахождение символьных выражений для сумм, в том числе и бесконечных можно выполнить с помощью функции SYMSUM(S,n,a,b), где S – слагаемое в символьном виде, n – переменная, верхний и нижний предел суммы.

Пример: Вычислить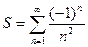

>> syms n

>> S=symsum('(-1)^n/n^2',n,1,inf)

S = -1/12*pi^2

Возможно суммирование слагаемых, зависящих не только от индекса, но и от некоторой символической переменной.

Пример: Найти значение бесконечной суммы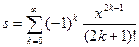

>> s=symsum((-1)^k*x^(2*k+1)/sym('(2*k+1)!'),k,0,inf)

s = sin(x)

Дата добавления: 2014-01-04