Длина дуги плоской кривой

Пусть в прямоугольных координатах дана плоская кривая 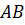уравнение которой 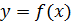, где . Длину дуги 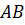будем рассматривать как предел, к которому стремится длина ломаной линии вписанной в эту дугу, когда число её звеньев неограниченно возрастает. Разобьем отрезок на частей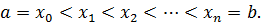

Пусть этим точкам соответствуют точки (рис. 100).

Проведем хорды 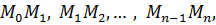длины которых обозначим соответственно По теореме Пифагора

где Тогда длина всей ломаной будет равна
По теореме Лагранжа

тогда
Переходя к пределу, мы получим

Найдем значение производной

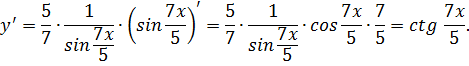
Таким образом

Воспользуемся вычислением в лекции 17 интеграла

Поэтому

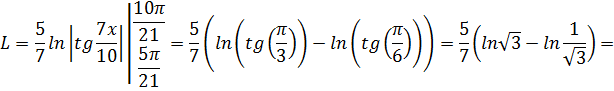
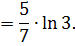
Если уравнение кривой 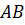задано в параметрическом виде

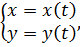
где , то формула длины кривой имеет вид

Пример 101. Найти длину дуги кривой , заданной параметрическими уравнениями

где

Решение. В нашем случае 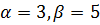и

Найдем значения производных

Таким образом

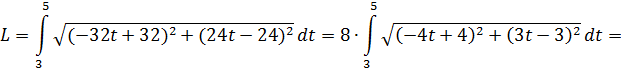
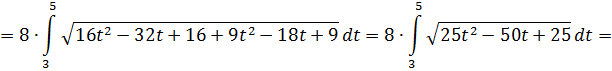
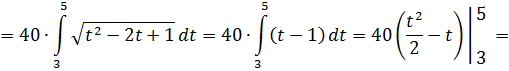
Применение интегрального вычисления в экономике.

Дата добавления: 2014-01-04