С нагрузкой статического характера

Расчет несимметричных режимов трехфазных цепей

Трехфазные электрические двигатели при конструктивной симметрии магнитной цепи и симметричной системе напряжения питания можно заменять эквивалентными схемами, состоящими из трех одинаковых сопротивлений, соединяемых «звездой» или «треугольником». При несимметрии напряжения питания, а также при конструктивной несимметрии машины такая экви­валентная замена оказывается недопустимой вследствие возникающего влияния режима работы (например, частоты вращения) на величину составляющих комп­лексного сопротивления отдельных фаз. Поэтому несимметричные режи­мы трехфазных цепей приходится рассчитывать иными методами, среди которых большое развитие получил метод симметричных составляющих, который будет рассмотрен позднее. Сейчас будем рассматривать несим­метричный режим цепей при условии так называемой статической нагрузки, т.е. такой нагрузки, когда сопротивления фаз различны, но независимы от протекающего тока и не влияют друг на друга. Кроме того, не будем учитывать падения напряжения на внутренних сопротивлениях фаз источника. Схема цепи представлена на рис. 7.15.

Пусть известна несимметричная система фазных напряжений источника 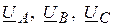. Неучет падений напряжения на внутренних сопротивлениях фаз источника позволяет заданные напряжения приписать ЭДС самого источника, т.е. положить 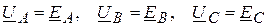. В этой схеме два узла, поэтому для определения напряжения между нулевыми точками приемника и источника можно применить метод двух узлов. Положив j _N = 0, будем иметь

, (7.8)

где 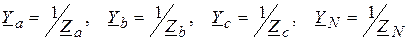– проводимости ветвей, присоединенных к узлу n.

Зная напряжение между нейтральными точками и учитывая равенство j _N = 0, можно найти токи в линиях по закону Ома:

,

,

,

,

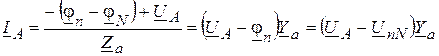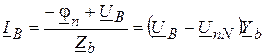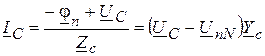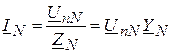Векторная и топографическая диаграмма напряжений, соответствующая одному из возможных несимметричных режимов, изображена на рис.7.16.

Интерес представляют два предельных случая.

Случай 1. Нулевые точки источника и приемника соединены толстым медным проводом, а расстояние между ними настолько мало, что можно считать .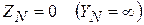

В этом случае U _nN = 0 и, следовательно, напряжения на фазах приемника равны фазным напряжениям источника питания (U _A = U _a, U _B = U _b, U _C = U _c). Ток в каждой фазе может быть рассчитан по закону Ома независимо от токов других фаз. (Расчет становится похожим на расчет токов в симметричной системе, однако его необходимо выполнять для всех трех фаз, а не для одной.)

Случай 2. Нейтральный провод отсутствует 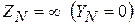. При этом

,

и расчет можно выполнять по изложенной методике, если заданными являются фазные напряжения. Однако чаще задаются не фазные, а линейные напряжения 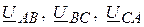(рис. 7.17). В этом случае приходится идти другим путем.

Обозначим напряжения на фазах нагрузки:

;

;

.

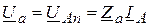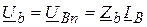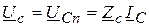Отсюда

;

;

.

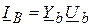В соответствии с первым законом Кирхгофа .

Подставив сюда значения токов, будем иметь: .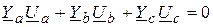

Из рассмотрения контуров AnB и AnC имеем два контурных уравнения

;

.

Отсюда

;

.

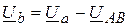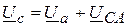Подставив в узловое уравнение, получим

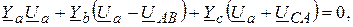
или

.

Тогда фазное напряжение U _a будет равно

.

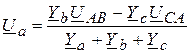Рассматривая другие контуры и составляя для них уравнения, после ана­ло­гичных преобразований получим

; .

Зная фазные напряжения и нагрузки фаз, находим токи

.

Рассмотрим расчет несимметричной нагрузки, соединенной «треугольником» (рис. 7.18).

	Рис. 7.18. Схема для расчета несимметричной нагрузки

Обычно задаются линейные напряжения .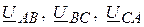

Фазные токи будут равны

.

Линейные токи определяются из выражений

;

;

.

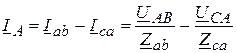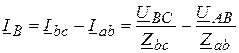Дата добавления: 2014-01-04