Функции построения гистограмм

Для построения гистограмм распределения в MATLAB предусмотрены функции:

hist(x,n), где n – количество интервалов разбиения;

Для коррекции центра ячеек: >>center=[x₁, x₂, x₃,… x_n] – задаётся матрица центра ячеек

>>hist(x, center)

bar(x,y,h), h – ширина колонки.

Пример:

>> randn (10000,1);

>> hist(x,n)

По заданным командам система производит следующие действия:

1. Генерирует с помощью функции randn вектор, состоящий из 10 000 случайных чисел, распределенных по нормальному закону.

2. Разобьет интервал, которому принадлежат эти числа, на n (по умолчанию десять) равных подинтервалов.

3. Вычислит количество чисел попавших в тот или иной подинтервал.

4. Построит гистограмму попадания случайных чисел в каждый интервал.

Polyarea(x,y) – возвращает площадь полигона заданного вершинами, находящихся в векторах x,y.

>> L=linspace(0,2*pi); >> X=cos(L)';Y=sin(L)'; >> A=polyarea(X,Y) A = 3.1395 >> plot(X,Y,'m')

Inpolygon(X,Y,xv,yv) – возвращает матрицу того же размера, что X,Y. Каждый элемент матрицы принимает одно из значений 1.0,5.0 в зависимости принадлежит ли точка с координатами(X(p,q) Y(p,q)0 полигону, вершины которого определяются векторами xv,yv: 1 – точка внутри полигона; 0,5 – на границе; 0 – вне полигона.

>> L=linspace(0.2*pi,8); >> yv=sin(L)'; >> xv=cos(L)'; >> x=randn(100,1);y=randn(100,1); >> IN=inpolygon(x,y,xv,yv); >> plot(xv,yv,'k',x(IN),y(IN),'r',x(~IN),y(~IN),'b*')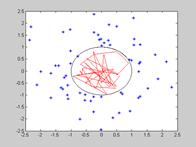

stairs (X,Y) – построение зависимости в ступенчатом виде по оси абсцисс Х, ординат У.

linspace(x1,x2,n) – генерирует вектор из n значений (по умолчанию 100), расположенных равномерно между х1 и х2

Пример: Результаты наблюдений над количественными признаками сведены в таблицу

хi
ni

Найти: 1) выборочную среднюю; 2) выборочную дисперсию; 3) исправленную выборочную дисперсию; 4) исправленное средне квадратичное исправление; 5) размах вариации, моду, медиану; 6)полигон частот

Решение:

1)

>> x=[2 6 10 12 14];

>> n=[1 5 7 3 4];

>> xv=1/sum(n)*sum(x. *n)

xv = 9.7000

2)

>> D=1/sum(n)*sum(x. ^2. *n))-xv^2 функция var (x,p) – вычисляет дисперсию

D = 10.9100

3)

>> Skv=sum(n)/(sum(n)-1)*D

Skv = 11.4842

4)

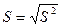
>> s=sqrt(Skv)

s = 3.3888

5)>> R=max(x)-min(x)

R = 12 % размах выборки

>> median(x)

ans = 10 % медиана

Мода М₀ - варианта, имеющая наибольшую относительную частоту = 10

6)

>> plot(x,n) >> axis([0 20 0 20]) >> xlabel('x');ylabel('n') >> grid on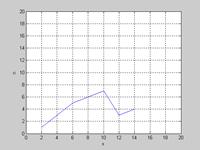

Пример:. Обработка выборки малого объёма

% Исходная выборка

x=[10,10,10,30,20,12,10,12,20,10];

% Объём выборки

n=length(x);

% Вариационный ряд для исходной выборки

Y=sort(x) Y = 10 10 10 10 10 12 12 20 20 30

% Построение статистического ряда

% повторяющиеся элементы

X=[10,12,20,30] X = 10 12 20 30

% Количество повторяющихся элементов

k=length(X);

% Абсолютные частоты для элементов вектора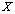

m=[0,0,0,0];

for i=1:k, for j=1:n,

if Y(j)==X(i), m(i)=m(i)+1; end

end, end

m

m = 5 2 2 1

% Относительные частоты

p=m/n

p = 0.5000 0.2000 0.2000 0.1000

% График статистической функции распределения

f=cumsum(p), stairs(X,f), pause

f = 0.5000 0.7000 0.9000 1.0000

Дата добавления: 2014-01-04