Интервальное оценивание параметров распределения

Оценку неизвестного параметра θ одним числом называют точечной. Будем обозначать выборочные параметры (точечные оценки) теми же буквами, что и соответствующие генеральные параметры, но с волной вверху. Выборочные математическое ожидание ~ m_x, дисперсия ~ D_x, среднеквадратичное отклонение ~σ _x, асимметрия ~ a_x и эксцесс ~ e_x определяется по формулам:

Пример:

>> x=[-2 1 2 3 4 5];

>> Mx=mean(x) % мат. ожидание

Mx = 2.1667

>> Sx=std(x) % с.к.о.

Sx = 2.4833

>> Dx= var(x) % дисперсия

Dx = 6.1667

>> n=length(x);

>> Ax=sum((x-Mx).^3)/(n-1)/Sx^3 % асимметрия

Ax = -0.5805

>> Ex=sum((x-Mx).^4)./(n-1)/Dx^2-3 % эксцесс

Ex = -1.0042

Оценка неизвестного параметра называется интервальной, если она определяется двумя числами – концами интервалов. Надёжностью оценки или доверительной вероятностью оценки называется вероятность γ, с которой осуществляется неравенство 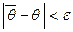, т.е. , где

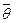- оценка; θ – оцениваемый параметр.

Число ε называют точностью оценки. Интервал 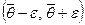, в котором с вероятностью γ содержится неизвестный параметр θ, называется доверительным.

По выборочным параметрам распределения можно найти доверительные интервалы для генеральных параметров. Доверительный интервал для генерального математического ожидания α СВ Х, распределённой по нормальному закону, имеет вид

t – значение аргумента функции Лапласа Ф(t), при котором Ф(t) = γ/2;

γ – доверительная вероятность (надёжность).

При неизвестном среднем квадратическом отклонении σ для оценки математического ожидания α СВ Х, распределенной по нормальному закону, служит доверительный интервал

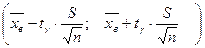
S – исправленное среднее квадратическое отклонение.

- находят по таблице по заданным n и γ.

Для оценки среднего квадратического отклонения σ нормально распределённого количественного признака Х с надёжностью γ по исправленному выборочному среднему квадратическому отклонению s служат доверительные интервалы:

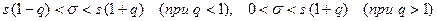
q- находят по таблице по заданным n и γ.

Дата добавления: 2014-01-04