Операторное изображение функций, их производных и интегралов

ОПЕРАТОРНЫМ МЕТОДОМ

РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ

При использовании операторного метода действительные функции времени, называемые оригиналами, заменяются операторными изображениями. Соответствие между оригиналом и изображением устанавливается с помощью некоторого функционального преобразования. Это преобразование выбирается так, чтобы операции интегрирования и дифференцирования оригиналов заменялись алгебраическими операциями над их изображениями. В этом случае дифференциальные уравнения для оригиналов переводят в алгебраические для их изображений.

Связь между оригиналом f (t) и его изображением устанавливается с помощью интеграла Лапласа:

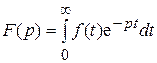, (10.1)

где p = G + j h – комплексное число.

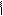Операторное изображение действительной функции f (t) является функцией комплексного числа p.

Для того чтобы интеграл Лапласа имел конечное значение, функция f (t) должна удовлетворять определенным условиям. Она должна удовлетворять условиям Дирихле: за любой конечный промежуток времени иметь конечное число разрывов первого рода и конечное число максимумов и минимумов. Кроме того, будем считать, что при t > 0 удовлетворяется условие: , где A и a – некоторые положительные числа. Все реальные токи и напряжения удовлетворяют этим условиям. Для того чтобы интеграл Лапласа имел конечное значение, необходимо полагать G > a.

Комплексное число p называют оператором.

Условимся записывать преобразование Лапласа в виде

F (p) = L [ f (t)]. (10.2)

Соответствие между оригиналом и изображением

F (p):= f (t). (10.3)

По определению, преобразование Лапласа применимо с момента t = 0₊. Обозначая значение функции и ее производных 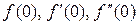и т.д., будем понимать под ними их значение при t = 0₊.

Существует обратное функциональное преобразование Лапласа, по которому можно определить оригинал, зная его изображение. Его называют обратным преобразованием Лапласа:

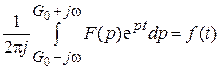, (10.4)

где p = G ₀ + j h.

Обратное преобразование Лапласа кратко записывается в виде

L ^–1[ F (p)] = f (t). (10.5)

Соттветствие некоторых характерных функций и их изображений приведено приложении.

В электротехнике распространено также функциональное преобра­зование, называемое преобразованием по Карсону:

. (10.6)

Достоинством преобразования по Карсону является одинаковость размерностей оригинала и изображения. При преобразовании Лапласа размерность изображения равна размерности оригинала, умноженной на размерность времени.

Достоинством преобразования по Лапласу является его соответствие с преобразованием Фурье, на котором основывается широко используемый в настоящее время частотный метод анализа цепей. В дальнейшем будем использовать преобразование Лапласа.

Преобразование производной

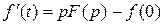. (10.7)

Изображение второй производной

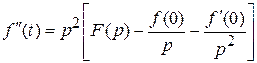. (10.8)

Изображение производной n -го порядка

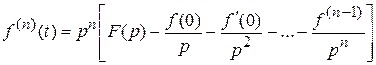. (10.9)

При нулевых начальных значениях

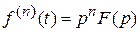. (10.10)

Изображение интеграла

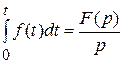. (10.11)

В дифференциальных уравнениях электрических цепей с производной во времени чаще всего встречаемся в напряжении на катушке: . Операторное изображение для u_L

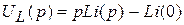. (10.12)

С интегралом чаще всего встречаемся в выражении напряжения на конденсаторе: .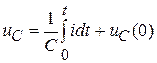

Изображение по Лапласу

, (10.13)

где U_C (0)/ p – изображение постоянной величины u_C (0).

Таким образом, при составлении уравнений цепи в операторной форме автоматически будут учитываться физические начальные условия – значения токов в катушках и напряжений на конденсаторах при t = 0.

Соответствие некоторых наиболее часто встречающихся функций их изображениям приведено в приложении. Более полно таблицы соответствия оригиналов и изображений приведены в справочниках по высшей математике.

При использовании преобразования Карсона следует умножить все изображения на p.

Изображение функции, смещенной во времени на величину x:

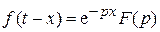. (10.14)

Если изображение смещено в комплексной плоскости на комплексное число a, то

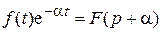. (10.15)

Дата добавления: 2014-01-04