Уравнения линии с распределенными параметрами

Понятие об электрических цепях с распределенными параметрами

ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

ЛЕКЦИЯ №36

Строго говоря, всегда параметры электрической цепи в той или иной степени распределены вдоль ее участков, и только абстрагируясь от действительности можно предполагать, что такие параметры цепи как активное сопротивление – R, индуктивность – L и емкость – C сосредоточены в ее определенных участках. Во многих случаях такое допущение не приводит к существенным ошибкам в результатах проводимого анализа. Ранее мы имели дело с цепями с сосредоточенными параметрами. Однако, такой подход не всегда возможен. Например, рассматривая электромагнитные процессы, происходящие в электрических линиях, при помощи которых электрическая энергия или сигналы передаются на расстояние, необходимо иметь ввиду, что электрические и магнитные поля распределены по всей длине линии, и превращение электрической энергии в тепло также происходит по всей длине линии. Критерием необходимости рассматривать цепь в качестве цепи с распределенными параметрами является то, что интервал времени распространения электромагнитной волны вдоль всей цепи и интервал времени, в течение которого токи и напряжения меняются на заметную величину, должны быть соизмеримыми.

Токи напряжения в таких цепях являются функциями двух независимых переменных: времени – t и расстояния – x, отсчитываемого вдоль направления цепи. Уравнения, описывающие процессы в таких цепях, являются уравнениями в частных производных. Примерами являются линии передачи электрической энергии, линии связи, антенные вводы радиотехнических устройств, обмотки электрических машин при воздействии на них импульсных токов и напряжений.

Параметры цепи могут быть распределены неравномерно вдоль линии.

Однако во многих случаях этим можно пренебречь и считать параметры равномерно распределенными. Такие линии называются однородными.

В дальнейшем под величинами R, L, C, G, M будем понимать активное сопротивление, индуктивность и т.д., приходящиеся на единицу длины, и будем обозначать их через R ₀, L ₀, C ₀, G ₀, M ₀. В общем случае эти параметры зависят от частоты, например, увеличение активного сопротивления и индуктивности с ростом частоты вследствие поверхностного эффекта. Однако для простоты в дальнейшем это учитывать не будем.

Напряжения и ток в линии являются функциями двух независимых переменных – пространственной координаты x, определяющей место наблюдения, и времени t, определяющей момент наблюдения. Считается, что направление координаты x совпадает с осью линии.

Необходимо найти пространственно-временное распределение величины тока в линии i (x, t) и напряжения между проводами u (x, t). В этом случае также можно определить процесс передачи энергии по линии, когда приемники и источники находятся на обоих концах линии.

Приняв положительное направление тока в линии слева направо, условимся называть "началом" левый конец линии. Расстояние от начальной точки до произвольной обозначим через x, а от конца – через x '. Вся длина линии l = x + x '.

Выделим элементарный участок D x на расстоянии x от начала. Пользуясь первичными параметрами R ₀, L ₀, C ₀, G ₀, отнесенными к единице длины линии, представим приближенно участок D x в виде схемы замещения (рис. 13.1).

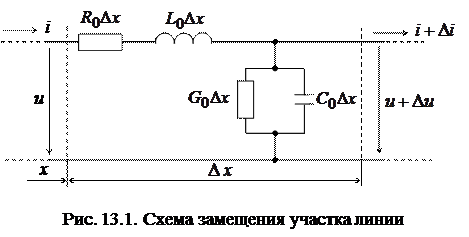Обозначим:

u – напряжение между верхним и нижним проводом в точке x;

D u – приращение напряжения на участке D x;

i – ток в точке x;

D i – приращение тока на участке D x.

Уравнения для приращений напряжения и тока на элементе D x линии запишутся:

(13.1)

Это уравнение в частных производных. По мере стремления D x к нулю степень точности этих уравнений повышается, причем величина второго порядка малости 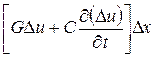в правой части второго уравнения может быть опущена.

В этом случае длинная линия рассматривается как цепная схема с бесконечно большим количеством звеньев, электрические параметры которых бесконечно малы.

Разделив обе части уравнений на D x и перейдя к пределу D x ® 0, получим дифференциальные уравнения линии

(13.2)

Эти уравнения носят название телеграфных.

Если за начало отсчета принять конец линии, т.е. ввести координату x ', уравнения примут вид:

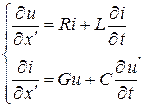(13.3)

Уравнения (13.2) и (13.3) решаются однозначно при использовании начальных и граничных условий. Начальными условиями будут служить значения напряжения и тока в начале и конце линии в момент времени, принятый за нуль. Граничные условия определяются связями между напряжением и током в начале или в конце линии и зависят от заданного режима работы линии.

Дата добавления: 2014-01-04