Формы записи уравнений Максвелла

ЛЕКЦИЯ №43

Уравнения Максвелла являются фундаментальными уравнениями электромагнитного поля. Эти уравнения могут быть записаны в интегральной, дифференциальной или комплексной форме. Интегральная форма записи уравнений устанавливает связь между величинами в разных точках поля или на разных отрезках, поверхностях. Дифференциальная форма описывает соотношение между величинами вблизи одной и той же точки поля в определенный момент времени. Эту форму записи применяют при исследовании полей, изменяющихся от точки к точке. Гармонически изменяющиеся электромагнитные поля (когда проекции вектора на координатные оси являются гармоническими функциями времени) удобно характеризовать уравнениями Максвелла в комплексной форме.

Переход от интегральной формы записи уравнений к дифференциальной осуществляется с помощью теорем Остроградского-Гаусса и Стокса (14.20) и (14.21).

Система уравнений электромагнитного поля включает в себя четыре основных уравнения Максвелла и уравнения связи между векторами поля и параметрами 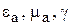, характеризующими свойства среды.

1. Закон полного тока – первое уравнение Максвелла

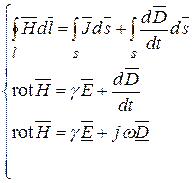. (14.37)

Ток смещения 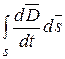, также как и ток проводимости 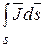, создает магнитное поле. Изменяющееся во времени электрическое поле создает магнитное поле. Направление вектора напряженности магнитного поля 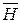связано с направлением полного тока и определяется правилом правоходового винта.

2. Закон электромагнитной индукции – второе уравнение Максвелла

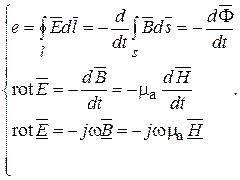(14.38)

Изменение магнитной индукции во времени создает электрическое поле, направление которого связано с направлением 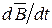и определяется правилом левоходового винта.

3. Принцип непрерывности магнитных силовых линий

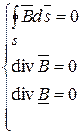. (14.39)

Магнитный поток через замкнутую поверхность равен нулю. Магнитные силовые линии всегда замкнуты и не имеют ни истоков, ни стоков.

4. Обобщенная теорема Гаусса

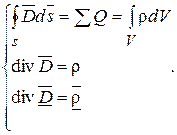(14.40)

Поток вектора электрического смещения через замкнутую поверхность равен алгебраической сумме свободных зарядов, находящихся внутри замкнутой поверхности.

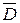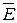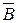5. Уравнения связи между векторами и 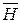, 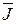и , и 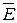в материальной среде

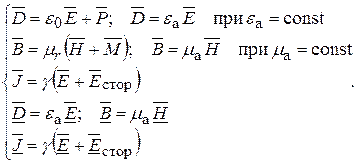. (14.41)

Дата добавления: 2014-01-04