Поле заряженной оси

И методов их решения

Общая характеристика задач электростатики

В зависимости от того, что задано и что необходимо определить, задачи электростатики можно подразделить на три типа.

1. По заданному закону распределения потенциала в пространстве j(x, y, z) найти распределение свободных зарядов, вызвавших поле.

Такого рода задачи можно решать с помощью уравнений Пуассона. Это наиболее простой тип задач.

2. Задан закон распределения свободных зарядов в пространстве в функции координат r_своб(x, y, z). Требуется найти закон изменения потенциала в пространстве j(x, y, z).

Эта задача является обратной по отношению к первой и значительно сложнее ее.

Принципиально задача состоит в решении уравнения Пуассона относительно j, т.е. в решении дифференциального уравнения второго порядка в частных производных.

Задачи первого и второго типа на практике встречаются редко, чаще приходится иметь дело с задачами третьего типа.

3. Известны потенциалы (или полные заряды) и геометрия тел, создающих поле. Требуется найти закон изменения напряженности или потенциала во всех точках поля.

Если среда, в которой создано поле, является неоднородной, то ее подразделяют на однородные области, и решение уравнения Лапласа производят для каждой области отдельно. Основная трудность задачи состоит в том, что хотя полные заряды тел и известны, но плотность распределения зарядов на отдельных участках заряженного тела неизвестна. Решения уравнений Лапласа для отдельных областей должны быть согласованы друг с другом: на границе раздела двух сред с различными диэлектрическими проницаемостями должны выполняться граничные условия.

Задачи третьего типа можно решать аналитически, графически либо путем моделирования.

Под заряженной осью понимают тонкий, теоретически бесконечно длинный металлический проводник.

Под линейной плотностью заряда t понимают заряд, приходящийся на единицу длины оси.

Пусть диэлектрическая проницаемость окружающей среды равна e_a.

Для нахождения напряженности поля в некоторой точке, удаленной на расстояние r от оси, проведем через точку цилиндрическую поверхность так, чтобы ее ось совпала с заряженной осью (рис. 15.6).

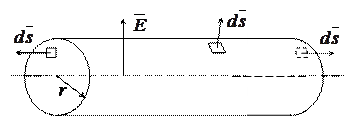Рис. 15.6. К определению поля заряженной оси

Используем теорему Гаусса, которая применима к замкнутой поверхности (боковая поверхность цилиндра и два его основания). Поток вектора 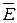имеется только через боковую поверхность. Направление 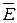и 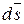на боковой поверхности в каждой точке совпадают, поэтому

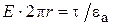
или

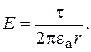(15.25)

Напряженность в поле заряженной оси изменяется обратно пропорционально расстоянию r точки от оси.

(15.26)

Потенциал изменяется по экспоненциальному закону.

Электрическая емкость определяется как отношение заряда к разности потенциалов между телами. Рассчитаем емкость двух соосных цилиндров (рис. 15.7).

Рис. 15.7. Разрез двух соосных цилиндров

Напряжение между поверхностями цилиндров

.

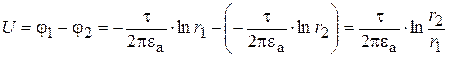Емкость цилиндрического конденсатора будет равна

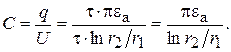(15.27)

Дата добавления: 2014-01-04