Поле заряженной оси, расположенной вблизи проводящей плоскости

Метод зеркальных отражений

ЛЕКЦИЯ №45

Этот метод применяется для расчета электростатических полей, ограниченных какой-либо проводящей поверхностью правильной формы или в которых есть геометрически правильная форма границы между двумя диэлектриками.

При использовании этого метода кроме заданного заряда вводят дополнительные (фиктивные) заряды, величина и месторасположение которых выбираются так, чтобы выполнялись граничные условия.

Этот метод можно использовать для расчета электрических полей в проводящей среде и магнитных полей.

Ось расположена параллельно плоскости на расстоянии h от нее (рис. 15.10). Требуется определить характер поля в диэлектрике.

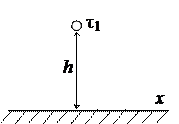Рис. 15.10. Ось вблизи проводящей поверхности

В результате электростатической индукции на поверхности проводящего тела выступают заряды. Плотность их меняется с изменением координаты x. Поле в диэлектрике создается всеми зарядами.

Для расчета поля в проводящую среду помещают фиктивный заряд на расстоянии h. При этом среда по обе стороны границы считается однородной (рис. 15.11).

Проводящая поверхность эквипотенциальна (j = const). Тогда потенциал ее равен

.

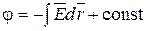При этом изменение потенциала вдоль поверхности

.

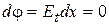Следовательно, граничным условием будет.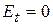

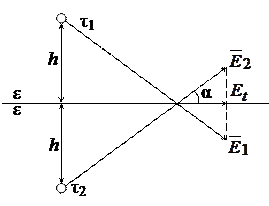Рис. 15.11. Расчетная схема

Тогда

.

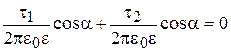Отсюда .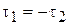

Потенциал в любой точке верхней полусферы будет равен

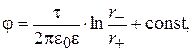(15.31)

где r _– – расстояние до отрицательно заряженной оси,

r ₊ – расстояние до положительно заряженной оси.

Потенциал провода

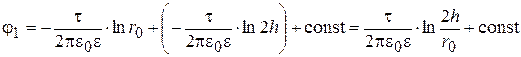, (15.32)

где r ₀ – радиус провода.

Разность потенциалов

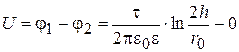(15.33)

.

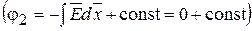Емкость провода

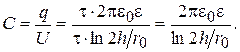(15.34)

Емкость провода относительно земли в два раза выше емкости двухпроводной линии.

Распределение заряда на границе раздела диэлектрика и проводника

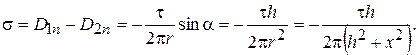(15.35)

Дата добавления: 2014-01-04