Возмущающее воздействие постоянно . В этом случае

Пусть задающее воздействие изменяется с постоянной скоростью

f=vt, v=const.

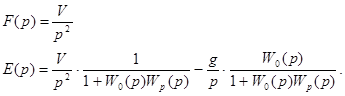
Относительно составляющей е₂ остается справедливым все сказанное ранее. Рассмотрим составляющую е₁. Ранее было показано,что:

е₁ =∞, если W(p) – статическая передаточная функция;

е₁=const≠0, если W(p) имеет астатизм первого порядка;

е₁=0, если W(p) имеет астатизм второго и выше порядков.

Таким образом, необходимо рассмотреть только случай, когда передаточная функция W(p) имеет астатизм 1-ог порядка. В этом случае

и при этом W^*(0)=1. Тогда

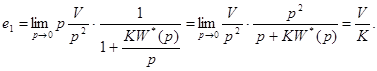(85)

Из () видно, что величина составляющей е₁ установившейся ошибки пропорциональна скорости изменения задающего воздействия и обратного пропорциональна коэффициенту передачи разомкнутой системы по скорости К.

Ошибка при движении с постоянным ускорением.

В этом режиме f(t)=dt², d – ускорение входного сигнала. Возмущающее воздействие g(t) предполагается постоянным и тогда составляющая е₂ та же, что и в первых случаях.

Рассмотрим составляющую е₁. очевидно, что, если:

W(p) – статическая передаточная функция или передаточная функция или передаточная функция с астатизмом 1-ог порядка – е₁=∞;

W(p) – передаточная функция с астатизмом 2-ог порядка, то е₁=const≠0;

W(p) имеет астатизм 3-ог и выше порядков, то е₁=0.

Поэтому остается рассмотреть только случай астатизма 2-го порядка.

При этом имеем

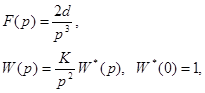
и

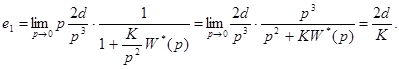
Ошибка при гармоническом задающем воздействии.

Этот режим движения рассматривается часто, т.к. он позволяет достаточно полно оценить динамические свойства САУ. Задающее воздействие имеет вид

f(t)=A sin wt.

Возмущающее воздействие рассматривать не будем (если оно постоянное, то все сказанное выше относительно составляющей е₂ полностью переноситься на этот случай.

Рассмотрим составляющую ошибки, определяемую наличием задающего воздействия. Имеем

В линейной системе при гармоническом входном сигнале ошибка изменяется по гармоническому закону, т.е.

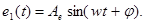
Точность САУ может быть оценена по амплитуде ошибки А_е; определяемой выражением

Обычно А_е много меньше амплитуды задающего воздействия А, т.е. 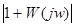- большая величина. Тогда

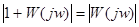
и

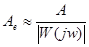(86)

Зависимостью () определяем амплитуду сигнала ошибки при гармоническом входном сигнале и оно же позволяет решить обратную задачу, т.е. сформировать требование к ЛАФЧХ разомкнутой системы, при выполнении которых амплитуда А_е не превосходит заданной величины ∆m. Имеем из (86)

(87)

откуда

и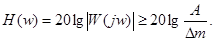

Значения (w, 20lg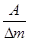) определяет точку на плоскости ЛАЧХ разомкнутой системы. Для выполнения условия (87) ЛАЧХ системы должна проходить выше этой точки (см. рис.82).

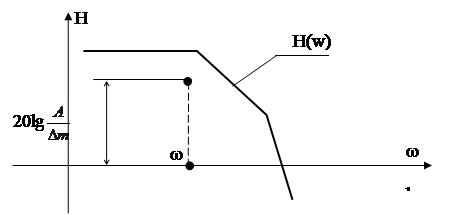Рис.82.

Дата добавления: 2014-01-04