Интегрирующие звенья

Интегрирующие звенья подразделяются на идеальные и реальные. Общим свойством этих звеньев является пропорциональность производной от выходной величины мгновенному значению входной величины. У реального интегрирующего звена пропорциональность устанавливается после завершения переходного процесса в звене.

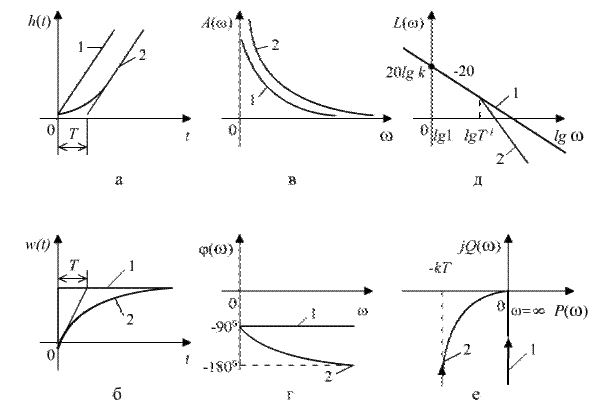
Рис. 3.6. Характеристики идеального (1) и реального (2) интегрирующих звеньев

Идеальному интегрирующему звену соответствует уравнение

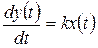(44)

Уравнению (3.44) соответствует интегральное уравнение

(45)

из которого видно, что звено интегрирует входной сигнал.

Переходную функцию получим из (3.45), полагая x (t)=1(t) (рис. 3.6, а):

h (t)= kt 1(t) (46)

Импульсная переходная функция идеального интегрирующего звена (рис. 3.6, б)

w (t)= k 1(t) (47)

Передаточная функция идеального интегрирующего звена

W (p)= k / p (48)

А.ф.х. идеального звена

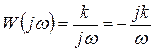(49)

на комплексной плоскости (рис. 3.6, е) представляет собой прямую, совпадающую с мнимой осью.

А.ч.х. (рис. 3.6, в)

(50)

является гиперболой, стремящейся к бесконечности при ω→0.

Ф.ч.х. идеального интегрирующего звена (рис. 3.6, г)

(51)

свидетельствует, что фазовый сдвиг не зависит от частоты и равен -90°.

Л.а.ч.х. представляет собой прямую с наклоном –20 дБ/декаду и проходит через точки ω=1; L (ω)=20lg k (рис. 3.6, д):

L (ω)=20lg A (ω)=20lg k – 20lgω (52)

Дифференциальное уравнение реального интегрирующего звена

(53)

а передаточная функция

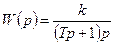(54)

Звено с передаточной функцией (3.54) может рассматриваться как последовательное соединение идеального интегрирующего звена с передаточной функцией 1/ p и статического инерционного звена первого порядка с постоянной времени T и коэффициентом передачи k. Все частотные характеристики реального интегрирующего звена могут быть получены по правилам перемножения комплексных величин.

Дата добавления: 2014-01-04