Звено запаздывания

Звеном запаздывания называется звено, передающее сигнал со входа на выход без искажения его формы, но с некоторой задержкой τ во времени. Наиболее распространенным в практике автоматических систем является транспортное запаздывание, обусловленное пространственным перемещением элементов, передающих информацию (например, транспортерная лента, полоса прокатываемого металла). К статическим устройствам запаздывания можно отнести различного рода линии задержки электронного или параметрического типа.

В некоторых случаях звено запаздывания вводится при расчете системы условно. Для ряда объектов уравнение динамики неизвестно, поэтому кривую переходного процесса реального объекта при единичном входном воздействии аппроксимируют экспонентой и эквивалентным запаздыванием.

Уравнение звена запаздывания

y (t)= x (t -τ) (64)

не является дифференциальным и относится к классу особых уравнений со смещенным аргументом.

Рис. 3.8. Характеристики звена запаздывания

Подстановкой в уравнение звена значения входной величины x (t)=1(t) получим его переходную функцию:

h (t)=1(t -τ) (65)

а подстановкой x (t)=δ(t) – импульсную:

w (t)=δ(t -τ) (65)

Временные характеристики звена запаздывания показаны на рис. 3.8, а, б.

На основании теоремы запаздывания запишем уравнение (3.64) в изображениях по Лапласу:

Y (p)= X (p) e ^{- p τ} (67)

и определим передаточную функцию звена как

W (p)= e ^{- p τ} (68)

А.ф.х. звена

W (j ω) = e ^{- j ωτ} = cosωτ - j sinωτ (69)

является окружностью единичного радиуса с центром в начале координат (рис. 3.8, е).

Амплитудная частотная и фазовая частотная характеристики определяются выражениями:

φ(ω) = arctg(-sinωτ / cosωτ) = -ωτ (70)

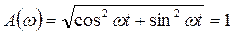(71)

Звенья запаздывания ухудшают устойчивость систем и делают их трудно управляемыми.

Дата добавления: 2014-01-04