Пример системы дифференциальных уравнений конвективного теплообмена

Запишем пример системы дифференциальных уравнений конвективного теплообмена. Пусть поверхность твердого тела омывается несжимаемой жидкостью (рис. 1), температура и скорость которой вдали от тела постоянны и равны, соответственно, t₀ и w₀. Размеры тела l₀ и другие заданы. Температура поверхности тела равна tc. Для определенности примем, что t_c >t₀.

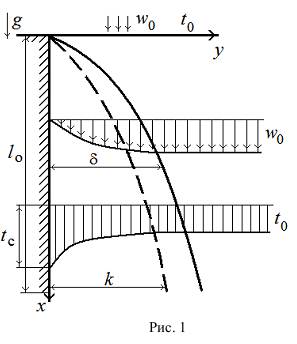
Будем полагать, что физические параметры жидкости постоянны (учтем только подъемную силу, возникающую в результате зависимости плотности от температуры). Теплота трения не учитывается. Рассматриваемый процесс является стационарным. Расположим оси координат так, как показано на рис. 1. Для простоты примем, что ось y нормальна к поверхности тела, а ось x направлена вдоль тела и вертикальна. При этом g_x=g, а проекции вектора силы тяжести (или подъемной силы) на оси y и z будут равны нулю(g_y= g_z = 0).

При принятых условиях конвективный теплообмен описывается системой дифференциальных уравнений (2), (3), (4), (5), для которой из-за стационарности процесса равны нулю частные производные по времени:

уравнение теплоотдачи (2):

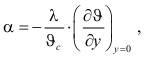
уравнение энергии (3):

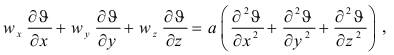
уравнение неразрывности (5):

уравнения движения (4):

Напишем граничные условия:

1) вдали от тела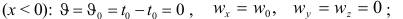

2) на поверхности тела

Контрольные вопросы

1. Сформулируйте закон Ньютона – Рихмана.

2. Запишите определение коэффициента теплоотдачи.

3. Перечислите виды конвекции и дайте их определение.

4. Каким процессом является теплоотдача – простым или сложным – и почему?

5. Перечислите теплофизические свойства жидкостей. Назовите порядок величины коэффициентов вязкости для воды и воздуха при комнатной температуре.

6. Является ли коэффициент теплоотдачи теплофизическим свойством и почему?

7. Запишите определение и единицы измерения динамической и кинематической вязкости.

8. Перечислите режимы течения жидкостей. Какое критериальное число их определяет?

9. Как и почему зависит теплоотдача от режимов течения жидкости?

10. Дайте определение гидродинамического и температурного пограничных слоев.

Дата добавления: 2014-01-04