Остаток в формуле Тейлора и его оценка

Производные n-го порядка вектор-функции, комплекснозначной и матричной функций

Если компоненты 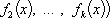n -кратно дифференцируемы, то .

Аналогично для комплекснозначной функции f и матричной функции A имеем формулы:

f ⁽ⁿ⁾(x) = u ⁽ⁿ⁾(x) + iv ⁽ⁿ⁾(x); dⁿf (x) = dⁿu (x) + idⁿv (x);

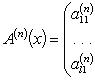
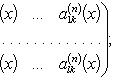
Разность между функцией и её многочленом Тейлора называется -м остатком, или -м остаточным членом; обозначим этот остаток через :

Формула , в более развёрнутой форме имеющая вид

называется формулой Тейлора для функции в точке 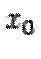, а представление функции в таком виде -- её разложением по формуле Тейлора.

Если считать, что остаток мал, то его можно отбросить без большой погрешности; при этом получается приближённая формула

дающая возможность для приближённого нахождения значений функции .

Выясним, в каком смысле можно понимать "малость" остатка в формуле Тейлора, чтобы этой приближённой формулой мы могли пользоваться осмысленно.

Теорема 1 (формула Тейлора с остаточным членом в форме Пеано) Пусть -- остаток в формуле Тейлора для функции 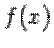в точке , и функция имеет непрерывную -ю производную. Тогда -- бесконечно малая величина того же или большего порядка малости, как , при . (Остаточный член , о котором известны эти сведения о порядке малости, называется остаточным членом в форме Пеано.)

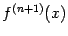Теорема 2 (остаток в формуле Тейлора в форме Лагранжа) Пусть при всех существует -я производная . Тогда для любого существует точка , лежащая между и (то есть при ), такая что

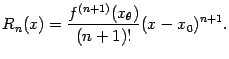
(Остаточный член формулы Тейлора, представленный в таком виде, называется остаточным членом в форме Лагранжа.)

Замечание 1 Полученную в предыдущей теореме оценку остатка удобно применять для оценки погрешности при замене функции её многочленом Тейлора, если известно, что -я производная при всех из рассматриваемого интервала ограничена по абсолютной величине некоторым числом:

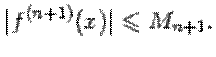
Тогда

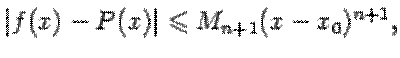
и при каждом фиксированном мы можем узнать оценку погрешности приближённой формулы .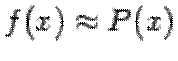

Замечание 2 Мы всюду подчёркивали, что приближённая формула имеет место только при малых значениях отклонения . Надежды на то, что при увеличении интервал, на котором можно будет применять с заданной точностью эту приближённую формулу, будет расширяться, вообще говоря, не оправдываются. Для пояснения сказанного приведём пример.

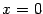Пусть рассматривается функция , доопределённая при по непрерывности: . Ранее мы уже рассматривали эту функцию и выяснили, что все её производные существуют на всей оси и при 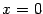равны 0: при всех . Это означает, что при любом порядке многочлена Тейлора все его коэффициенты равны 0, и формула Тейлора сводится к равенству . Таким образом, любой остаток в формуле Тейлора для этой функции в точке 0 равен одному и тому же, а именно, самой функции ! Поэтому уменьшить остаток за счёт увеличения здесь никак не возможно: единственным приближением, которое формула Тейлора даёт для функции , здесь служит тождественный 0.

Дата добавления: 2014-01-04