Тема: Елементи механіки абсолютно твердого тіла

Лекція № 10

Навчальність та її властивості. Класифікація школярів з низьким рівнем навчальних досягнень.

Психологи називають однією з основних причин невстигання - понижену навчальність. Навчальність - це більш-менш повний комплекс пізнавальних процесів, навчальних навичок, сформованих певною мірою,

ставлення до учіння та, передусім, легкість, швидкість оволодіння новими знаннями, тобто загальні розумові здібності до засвоєння знань. Виділяють загальну та спеціальну навчальність.

Існує досить багато підходів до класифікації школярів з шкільною неуспішністю. Найбільш узагальненою є така: 1) школярі, невстигання яких зумовлене порушеннями мотиваційної сфери учбової діяльності; 2) учні, неуспішність яких викликана порушенням цілепокладання учбової діяльності; 3) школярі, неуспішність яких зумовлена порушенням мотиваційного блоку учбової діяльності.

Розглянемо тверде тіло, яке може обертатися навколо вісі обертання і рухатися поступально. Його рух у загальному випадку визначається двома векторними рівняннями:

- рівняння руху центра мас: ;

- рівняння моментів у Ц-системі: .

Знаючи закони діючих зовнішніх сил, точки їхнього прикладу і початкові умови, можна за допомогою цих рівнянь знайти як швидкість, так і положення кожної точки твердого тіла в будь-який момент часу, тобто цілком розв’язати задачу про рух тіла.

Умови рівноваги твердого тіла.

Тіло буде залишатися в стані спокою, якщо відсутні причини, що викликають його рух. Для цього необхідно і достатньо виконання двох умов:

1. рівнодіюча всіх зовнішніх сил, які прикладені до тіла, повинна бути рівною нулю: ;

2. сумарний момент зовнішніх сил відносно будь-якої точки теж повинний бути рівним нулю: .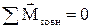

Ці умови повинні виконуватися в тій системі відліку, де тіло знаходиться в стані спокою. Якщо система відліку неінерціальна, то крім зовнішніх сил взаємодії треба враховувати і сили інерції. Це ж відноситься і до моментів сил.

Обертання тіла навколо нерухомої вісі.

Нехай тверде тіло обертається навколо нерухомої вісі. Визначимо вираження для моменту імпульсу твердого тіла відносно вісі обертання ОО'. Момент імпульсу тіла може бути представлений таким чином:

,

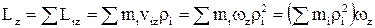де і 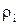– маса і відстань від вісі обертання і-ї частинки твердого тіла, – його кутова швидкість. Величина в дужках являє собою момент інерції твердого тіла відносно вісі ОО': . З останньої формули випливає, що момент інерції твердого тіла залежить від розподілу мас щодо цікавлячої нас вісі і є величиною аддитивною. Обчислення моменту інерції тіла проводиться за формулою:

,

де dm і dV – маса й об’єм елемента тіла, що знаходиться на відстані r від цікавлячої нас вісі Z, r – густина тіла в даній точці.

Якщо задано момент інерції відносно вісі, що проходить через центр мас, момент інерції відносно будь-якої вісі, паралельної даної і віддаленої від неї на відстань а, визначається за теоремою Штейнера: Момент інерції відносно довільної вісі Z дорівнює моментові інерції І_с відносно вісі Z_с, що паралельна даної і проходить через центр мас С тіла, плюс добуток маси m тіла на квадрат відстані а між вісями:

.

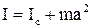Рівняння динаміки обертання твердого тіла.

Нехай тверде тіло обертається навколо нерухомої вісі. Проекція моменту імпульсу в цьому випадку визначається за формулою:

.

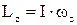Продифференціюємо останнє рівняння за часом:

або .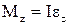

З останнього рівняння свідчить, що момент інерції визначає інерційні властивості твердого тіла при обертанні: при тому самому значенні моменту сил тіло з великим моментом інерції здобуває менше кутове прискорення.

Інтегрування отриманого рівняння з урахуванням початкових умов дозволяє цілком розв’язати задачу про обертання твердого тіла навколо нерухомої вісі, тобто знайти залежності кутової швидкості і кута повороту від часу.

Нехай e = const. Тоді 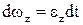, , 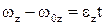. У підсумку рівняння залежності проекції кутової швидкості від часу має вигляд:

.

З формули кутової швидкості випливає: 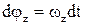, . Після інтегрування одержуємо рівняння обертального руху твердого тіла:

.

Робота зовнішніх сил при обертанні твердого тіла навколо нерухомої вісі.

При обертанні твердого тіла навколо нерухомої вісі обертання потенціальна енергія залишається сталою, тому робота всіх зовнішніх сил дорівнює зміні тільки кінетичної енергії тіла: 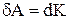. Оскільки 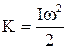, то після підстановки одержуємо: , (, так як вісь Z за напрямком збігається з кутовою швидкістю). Тоді і . Відповідно до основного рівняння динаміки обертального руху твердого тіла . Підставляючи останню формулу у вираження для механічної роботи і враховуючи, що 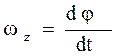, одержуємо: . Робота зовнішніх сил при повороті на кінцевий кут дорівнює 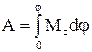. У випадку, якщо 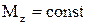, остання формула спрощується: .

Висновок: Робота зовнішніх сил при обертанні твердого тіла навколо нерухомої вісі визначається дією моменту цих сил відносно даної вісі. Якщо сили такі, що їхній момент 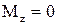, то роботи вони не виконують.

Плоский рух твердого тіла.

При плоскому русі центр мас С твердого тіла рухається у визначеній площині, що нерухома в даній К-системі відліку, а вектор його кутової швидкості увесь час залишається перпендикулярним до цій площині. Останнє означає, що в Ц-системі тверде тіло виконує чисто обертальний рух навколо нерухомої в цій системі вісі, що проходить через центр мас тіла. Обертальний рух твердого тіла визначається рівнянням 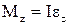, яке справедливо в будь-якій системі відліку.

Таким чином, плоский рух твердого тіла може бути описаним наступними двома рівняннями:

, ,

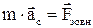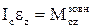де m – маса тіла, F – рівнодіюча всіх зовнішніх сил, і 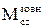– момент інерції і сумарний момент усіх зовнішніх сил відносно вісі, що проходить через центр мас тіла. Інтегруючи отримані рівняння з урахуванням початкових умов, можна знайти залежності и 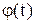, що визначають положення твердого тіла в будь–який момент t.

Кінетична енергія при плоскому русі твердого тіла.

Кінетична енергія при плоскому русі твердого тіла складається з енергії обертання в Ц–системі і енергії, що зв'язана з рухом центра мас:

.

Вільні вісі. Головні вісі тіла.

Якщо тверде тіло привести в обертання і потім надати самому собі, то напрямок вісі обертання в просторі буде змінюватися. Для того щоб довільна вісь обертання тіла зберігала свій напрямок незмінним, до неї необхідно прикласти визначені сили.

Нехай середина С однорідного стрижня жорстко скріплена з віссю обертання так, що кут між стрижнем і віссю дорівнює J. Знайдемо момент М зовнішніх сил, які необхідно прикласти до вісі обертання, щоб при обертанні стрижня з кутовою швидкістю w її напрямок не змінювався. Оскільки , то щоб визначити М, спочатку треба знайти момент імпульсу стрижня L, а потім його похідну за часом.

Виділимо на стрижні елемент маси dm, що знаходиться на відстані r від точки С. Його момент імпульсу відносно цієї точки 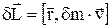, де v – швидкість елемента. Легко побачити, що вектор 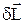спрямований перпендикулярно стрижневі, причому його напрямок не залежить від вибору елемента . Тому сумарний момент імпульсу стрижня збігається за напрямком з вектором 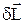і не збігається з вектором 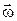. При обертанні стрижня вектор буде також обертатися з кутовою швидкістю w.

Таким чином, для утримання вісі обертання в незмінному напрямку до неї необхідно в даному випадку прикласти момент деяких зовнішніх сил. Однак, якщо J = p/2, то вектор 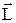збігається за напрямком з вектором 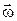, і в цьому випадку , тобто напрямок вісі обертання буде залишатися незмінним без зовнішнього впливу.

Вісь обертання, напрямок якої в просторі залишається незмінним без дії на неї яких–небудь сил ззовні, називають вільною віссю тіла.

У загальній теорії доводиться, що для будь–якого твердого тіла існують три взаємно перпендикулярні вісі, що проходять через його центр мас, і які можуть служити вільними осями. Їх називають головними осями тіла. Особливістю головних осей є те, що при обертанні тіла навколо кожної з них його момент імпульсу збігається за напрямком з кутовою швидкістю і визначається за формулою 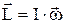, причому 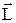не залежить від вибору точки, відносно якої його визначають.

Дата добавления: 2014-01-04