Сполучний закон додавання (асоціативний)

Переставний закон додавання (комутативний).

Для будь-яких цілих невід’ємних чисел а і в виконується рівність а+в=в+а.

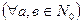
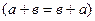
Доведення. Нехай 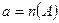, і 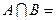○. Тоді за означенням суми цілих невід’ємних чисел: 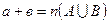, але .

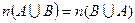отже .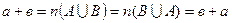

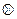
Для будь-яких цілих невід’ємних чисел а, в, с виконується рівність (а+в)+с=а+(в+с).

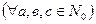
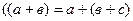
Доведення. Нехай 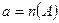, , 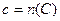і 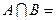○.○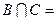 Тоді за означенням суми двох чисел можна записати 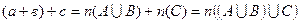. Але так як об’єднання множин володіє сполучною властивістю 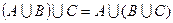, то 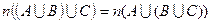. Тоді.

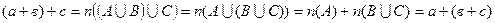Сполучна властивість дозволяє знаходити суму трьох доданків. Для цього достатньо додати перший доданок до другого і до одержанного числа додати третій доданок, або додати перший доданок до суми другого і третього.

Переставний і сполучний закони можуть бути узагальнені на будь-яке число долданків. При цьому переставна властивість буде означати, що сума не зміниться при будь-якій перестановці доданків, а сполучний – що сума не зміниться при будь-якій групіровці доданків (без зміни порядку).

Наприклад.

1. Обчисліть, застосовуючи закони додавання

219+361+281+164+52=

На основі переставної властивості переставимо доданки 36 і 281.

Тоді 219+36+281+164+52=219+281+36+164+52 =

(на основі сполучного закону згрупуємо доданки, а потім знайдемо суми у дужках)

=(219+281)+(36+164)+52=500+200+52 = (застосуємо ще раз сполучний закон) =

=(500+200)+52=700+52=752

З переставною властивістю учні знайомляться при вивченні додавання і віднімання в межах 10. Спочатку цей закон використовується при вивченні таблиць додавання. Наприклад, 5+6=6+5=11, 5+7=7+5=12. А потім вже для раціональних обчислень.

З сполучним законом учні знайомляться в 4-му класі і використовують придбані знання для раціональних обчислень.

Розв’язування вправ.

№1,ст.132

(4 + 5) + 6 = переставимо місцями доданки 4 і 5 застосувавши переставну властивість додавання = (5+4)+6 = застосуємо сполучний закон = 5 + (4 + 6)

№3, ст.132

(30 + 7) + (10 + 4) = 30 + 7 + 10 + 4 = 30 + 10 + 7 + 4 = (30 + 10) + (7 + 4) = 40 + 11 = 51

№4, ст.132

273 + 1227 + 154 + 446 = (123 + 1227) + (154 + 446) = 1500 + 600 = 2100

ІV. Визначення відношення «менше» через додавання.

З’ясуємо на якій теоретичній основі проходить порівняння чисел.

Нехай дано два цілі невід’ємні числа а і в. З теорети­ко-множинної точки зору вони представляють число елементів скінчених множин А і В: а=n(А), в=n(В). Якщо ці множини рівнопотужні, то їм відповідає одне і те ж число, тобто а=в.

Числа а і в рівні, якщо вони визначаються рівно потужними множинами:

 

Якщо множини А і В не рівнопотужні, то числа, які визначаються ними – різні.

Якщо множина А рівнопотужна своїй підмножині множини В та n(А)=а, n(В)=в, говорять, що число а менше числа в, та пишуть а<в.В цій же ситуації говорять, що в більше а, та пишуть: в>а

	а<в <=> А~В1, де В1 В та В1≠В, В1≠Ø

Із наведених визначеннях відношень «дорівнює» та «менше» виходять в початковій школі, коли пояснюють, що 2=2, 3=3, 2<3, 3<4 і т.д.

Н., при введенні запису 3=3 розглядають дві рівнопотужні множини квадратів та кругів.

 

 

 

При вивченні відношення 3 < 4 проводяться роздуми: візьмемо три рожевих кружечки та 4 синіх і кожний рожевий покладемо на синій, що синій кружечок залишився незакритим, тобто, рожевих кружечків менше, чим синіх, тому можна записати 3 < 4.

Відмітимо, ще, що якщо числа а і в визначаються відповідно множинами А та В (кругів, квадратів, паличок тощо) та а < в, то виділення в множині В особистої підмножини, рівнопотужна множині А, на практиці виникає самими різноманітними способами: накладанням, шляхом утворення пар і т.д. Це можливо, так як відношення а < в.

Цей підхід для визначення відношення «менше» має обмежене застосування, він може бути використаний для порівняння чисел в межах 20, оскільки пов'язаний з непосредственим порівнянням двох груп предметів.

Число а менше числа в тільки тоді, коли існує таке натуральне число с, що а + с = в

Користуючись цим визначенням можна пояснити, що 3 < 7. 3 < 7 – оскільки існує таке число 4, що 3 + 4 = 7.

Цей спосіб визначення відношення «менше» через додавання також використовується в початкових класах. Про це говорить наявність записів 5 + 1 = 6, 6 > 5, 7 + 1 = 8, 8 > 7.

Число а менше числа в тоді, коли відрізок натурального ряду N_а являється власною підмножиною відрізка цього ряду N_в.

	а<в <=> NаNв та Nа ≠ Nв

 

 

Н.: справедливість нерівності 3 < 7 із цих позицій можна пояснити тим, що {1, 2, 3}, {1, 2, 3, 4, 5, 6, 7}.

Дана трактовка поняття «менше» дозволяє порівняти числа, спираючись на знання їх місця в натуральному ряді.

Цей спосіб порівняння чисел також використовується в початкових класах: число, яке при рахунку зустрічається раніше, завжди менше числа, яке іде пізніше.

3. Заключна частина:

Загальний висновок.

Відповіді на запитання студентів.

Д/з: Стойлова Л.П., Пишкало А.М. Основы начального курса математики, Р. 2, п. 48 - 49, С. 128 – 132, впр. 3, 4 (С. 132).

Кухар В.М., Білий Б.М. Теоретичні основи початкового курсу математики. Р.V, § 4, с. 169 – 174 впр. 2, 3, 8 (С.174).