
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основні гіпотези
|
|
|
|
1. Перерізи, що були плоскі до деформації залишаються плоскими і після її виникнення.
2. Радіуси, що проведені в поперечних перерізах залишаються в процесі деформування прямими.
3. Відстані поміж поперечними перерізами залишаються без зміни.
Стержні що працюють на кручення називаються валами.
Любий переріз на відстані 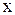 від защемлення під дією крутного моменту провертається на кут
від защемлення під дією крутного моменту провертається на кут 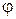 , що називається абсолютним кутом закручування. Залежність
, що називається абсолютним кутом закручування. Залежність 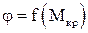 називається діаграмою деформування при крученні. Діаграма кручення має досить схожий вигляд з діаграмою при розтязі пластичних матеріалів.
називається діаграмою деформування при крученні. Діаграма кручення має досить схожий вигляд з діаграмою при розтязі пластичних матеріалів.
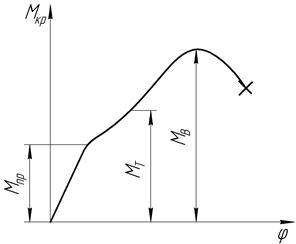 2. Оскільки нас цікавлять напруження в поперечних перерізах, що виникають на ділянці пропорційності, то розглянемо дану задачу виходячи з чотириєдиної задач її розв'язку.
2. Оскільки нас цікавлять напруження в поперечних перерізах, що виникають на ділянці пропорційності, то розглянемо дану задачу виходячи з чотириєдиної задач її розв'язку.
 1. Статична сторона задачі: запишемо необхідне інтегральне рівняння рівноваги:
1. Статична сторона задачі: запишемо необхідне інтегральне рівняння рівноваги:

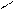

 , (1)
, (1)
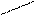
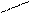
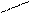
 де
де  - радіус в перерізі вала,
- радіус в перерізі вала,
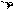

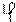





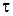 - напруження дотичні, що діють в заданому перерізі.
- напруження дотичні, що діють в заданому перерізі.
2. Геометрична сторона задачі:
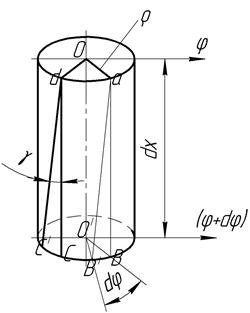 Розглянемо деформацію елемента, що знаходиться на відстані
Розглянемо деформацію елемента, що знаходиться на відстані 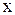 від закріплення. В ньому:
від закріплення. В ньому:  – радіус стержня в перерізі, що розглядається.
– радіус стержня в перерізі, що розглядається.
Таким чином деформація кручення на довжині 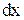 буде виражатись в зміні початкових прямих кутів
буде виражатись в зміні початкових прямих кутів 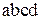 на кут
на кут 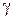 . Тобто елемент, що нами розглядається; під дією
. Тобто елемент, що нами розглядається; під дією 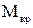 знаходиться в умовах чистого зсуву і відповідно на його гранях діють дотичні напруження
знаходиться в умовах чистого зсуву і відповідно на його гранях діють дотичні напруження 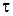 .
.
У силу цього кут (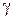 ) є кутом зсуву (відносний кут зсуву). І визначається як:
) є кутом зсуву (відносний кут зсуву). І визначається як: 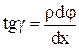 де
де 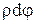 - довжина дуги круга радіуса
- довжина дуги круга радіуса  .
.
В силу того, що деформація дуже мала дугу замінюють відрізком прямої, a 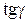 замінюється на просто
замінюється на просто 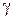 . Звідки:
. Звідки:
(2) 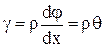 , де
, де 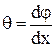 – відносний кут повороту одного перерізу по відношенню до іншого (см-1).
– відносний кут повороту одного перерізу по відношенню до іншого (см-1).
3. Фізична сторона задачі:
запишемо закон Гука: 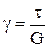 , а з другої сторони кут
, а з другої сторони кут 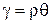 Þ
Þ 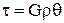 (3).
(3).
4. Синтез: Підставляємо в (1) рівняння (3):
 Þ
Þ
 (4);
(4); 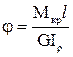 (5);
(5); 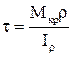 (6).
(6).
(4) – закон Гука в відносних величинах при крученні круглих стержнів (валів).
(5) – закон Гука в абсолютних величинах, що дозволяє визначити абсолютний кут закручення валу.
(6) – формула для визначення дотичних напружень в любій точці круглого перерізу.
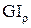 – жорсткість поперечного перерізу круглого валу при закрученні. [кН×м2].
– жорсткість поперечного перерізу круглого валу при закрученні. [кН×м2].
Користуватись формулою (2) можна тільки в випадках коли 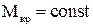 і
і 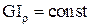 .
.
Якщо одна з цих умов не дотримується, то для визначення абсолютного кута закручення 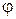 використовується залежність:
використовується залежність:
 ,
,
де 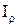 - полярний момент інерції, що для круглого поперечного перерізу дорівнює:
- полярний момент інерції, що для круглого поперечного перерізу дорівнює:
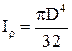
Приклад:
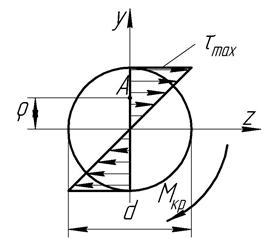
Розрахувати так дотичні напруження в довільній т. А, що знаходиться на відстані  від осі вала.
від осі вала.
Розв’язок:
1) 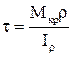 ;
; 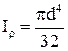 ;
;
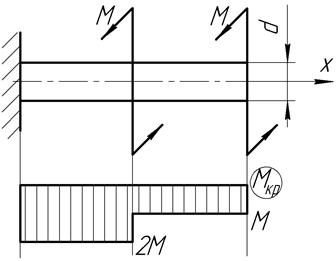
2) Будуємо епюру крутних моментів. Звідки знаходимо, що 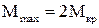 . Оскільки
. Оскільки 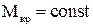 і
і 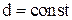 , то:
, то: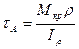 , при
, при 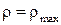 Þ
Þ
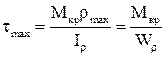
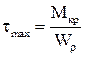 , де
, де 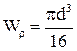
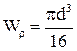 – полярний момент опору для круглого стержня.
– полярний момент опору для круглого стержня.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 477; Нарушение авторских прав?; Мы поможем в написании вашей работы!