Система двох випадкових величин

В практиці геодезичних вимірів досить часто взаємодіють дві випадкові величини Х та Y, тобто двомірні випадкові величини. Так, наприклад, координати точки на площині визначаються двома випадковими величинами: абсцисою Х та ординатою Y;положення точки в просторі визначається вже трьома координатами - Х, Y та висотою Н.

При лінійних вимірах взаємодіють - довжина мірного приладу та температура. При дослідженнях деформацій інженерних споруд взаємодіють - величина осідання та інтервал часу і так далі.

Закон розподілу системи двох випадкових величин задають функцією розподілу та щільністю розподілу.

Функцією розподілу системи двох випадкових величин називають функцію двох аргументів F (x,y), що дорівнює ймовірності сумісного виконання двох нерівностей X < x i Y < y, тобто

F (x,y) = P (X < x i Y < y). (2)

Геометрично функцією розподілу системи двох випадкових величин є ймовірність попадання випадкової точки (Х,Y) в нескінченний квадрат площини (рис. 1) з вершиною в точці (х,у).

Функція розподілу має такі властивості:

1. Якщо один із аргументів наближається до плюс нескінченності, то функція розподілу системи наближається до функції розподілу випадкової величини другого аргументу, тобто

F (x, +¥) = F ₁(x);

F (+¥, y) = F ₂(y).

2. Принаближенні обох аргументів до плюс нескінченності функція розподілу F (x,y) наближається до одиниці:

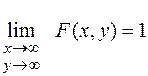, або F (+¥, +¥) = 1.

3. При наближенні одного чи обох аргументів до мінус нескінченності функція розподілу наближається до нуля:

,

або F (- ¥, у) = F (х, - ¥) = F (- ¥, - ¥) = 0.

4. Функція розподілу (F (х, у)є зростаючою функцією з кожного аргументу:

F (x ₂, y) ³ F (x ₁, y), якщо х ₂ > x ₁;

F (x, y ₂) ³ F (x, y ₁), якщо у ₂ > у ₁.

5. Ймовірність попадання випадкової точки (х,у) в будь-який прямокутник зі сторонами, паралельними координатним осям, обчислюється за формулою

F (x ₂, y ₂) - F (x ₁, y ₂) -

- F (x ₂, y ₁) + F (x ₁, y ₁).(3)

Це легко з’ясувати геометрично, якщо уявити положення прямокутника з координатами вершин А (x ₁, y ₁), В (x ₁, y ₂), С (x ₂, y ₂) і D (x ₂, y ₁) на рис. 1 і геометричними значеннями функцій F (x ₂, y ₂), …, F (x ₁, y ₁)в формулі (3).

Практичне значення мають системи неперервних випадкових величин, розподіл яких характеризують щільністю розподілу j(x, y). За допомогою неї більш просто знаходять імовірність попадання в різні області, а опис розподілу системи випадкових величин стає більш наочним.

Щільність розподілу системи двох випадкових неперервних величин визначають як другу змішану часткову похідну від функції F (x, y),тобто

j(х,у) = 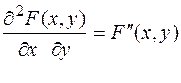. (4)

Геометрично функцію j(х,у)можна виразити просторовою поверхнею, що нагадує перевернутий до низу дзвоник, краї якого віддаляються до нескінченності, асимптотично наближаючись до площини х 0 у (рис. 2). Її називають поверхнею розподілу.

Рис. 1

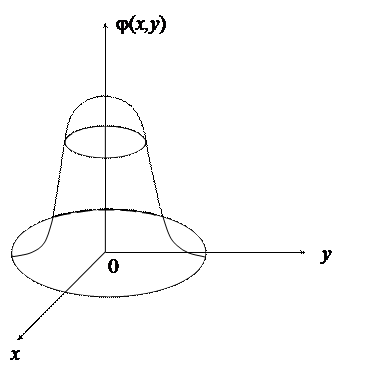
Рис. 2

Функція розподілу F (x,y) визначається за формулою

F(x,y) = j(x,y) dxdy. (5)

Щільність розподілу системи двох випадкових величин має властивості:

1.Щільністю розподілу є функція

j(x,y) ³ 0.

2.Подвійний інтеграл з нескінченними межами від функції щільності розподілу дорівнює одиниці:

j(x,y) dxdy = 1.

Геометрично це свідчить про те, що об’єм тіла, відмежованого поверхнею розподілу і площиною х 0 у, дорівнює одиниці.

Щільності розподілу величин х та у, що входять в систему, визначають за формулами:

j₁(х) = j(x,y) dy;

j₂ (у) = j(x,y) dх.

Тобто, для визначення щільності розподілу однієї із системи випадкових величин, треба проінтегрувати в необмежених межах щільність розподілу системи j(х,у)за аргументом другої випадкової величини.

Якщо відомі щільності розподілу окремих випадкових величин системи і випадкові величини х та у незалежні між собою, то можна визначити закон їх сумісного розподілу за формулою

j(х,у) = j₁(х) × j₂ (у).

Подібно умовній імовірності Р для подій визначають умовні щільності розподілу:

1) j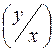-щільністьрозподілу y при умові, що випадкова величина Х прийняла значення х;

2) j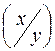- щільність розподілу х при умові, що випадкова величина Y прийняла значення у.

Дата добавления: 2014-01-04