Якщо вони взаємно залежні між собою, то

Закон її сумісного розподілу визначають за формулою

j(х,у) = j₁(х) j,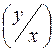

або j(х,у) = j₂(y) j.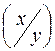

Випадкова величина Х буде незалежною від випадкової величини Y, якщо закон розподілу величини Х не залежить від прийнятого значення величини Y, тобто

j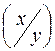= j₁(х),

і навпаки, для випадкової величини Y маємо

j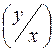= j₂(у).

j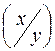¹ j₁(х);j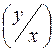¹ j₂(у).

Випадкові величини Х i Y незалежні, якщо щільність сумісного розподілу j(х,у)можна визначити у вигляді добутку двох множників, кожен із яких утримує тільки величини х та у, тобто

j(х,у) = .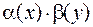

Додамо, що при розкладанні, функції 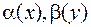з точністю до постійної множників збігаються з щільностями розподілу j₁(x) і j₂(у).

Між випадковими величинами виникає функціональна або стохастична (ймовірна)залежність.

Функціональною залежністю між випадковими величинами Х і Y називають таку залежність, коли кожному значенню Х відповідає точне значення Y.

Наприклад, у = х ², S = a×b і т.д.

Стохастичною (ймовірною) залежністю між випадковими величинами Х і Y називають таку залежність, при якій кожному значенню х можна вказати розподіл величини у, яке змінюється при зміні х.

Така залежність в практичній діяльності зустрічається досить часто. Наприклад, зріст та вага людини, висота і товщина дерева в лісі, величина деформації інженерних споруд, час їх експлуатації і т.д.

Тобто у випадку ймовірної залежності на кожне точне значення аргументу х можна вказати значення випадкової величини у з певною мірою ймовірності (Р_у).

Система двох випадкових величин може підкорятися різним законам розподілу. Проте в практиці геодезичних вимірювань найбільше розповсюдження має нормальний закон розподілу.

Якщо випадкові величини Х і Y мають нормальний розподіл і незалежні між собою, то щільності розподілу кожної із них будуть:

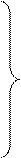j₁(х)= ;

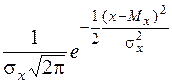(6)

j₂ (y) = .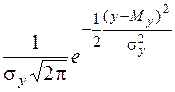

Згідно з формулою щільність розподілу системи (Х, Y), якщо випадкові величини Х та Y незалежні, отримаємо у вигляді

j(х,у) = 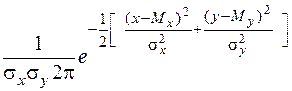. (7)

Якщо центр системи (х,у) знаходиться на початку системи координат х 0 у, тобто М_х = М_у = 0, то

j(х,у)= 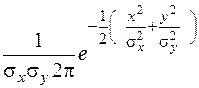. (8)

Поверхня щільності нормального розподілу системи (х,у) має опуклий вигляд (горб), показаний на рис. 2.

Ймовірність попадання випадкової точки в прямокутник із сторонами паралельними осям координат, в межі з координатами х ₁ ,х ₂і у ₁ ,y ₂ (рис. 1) визначається за формулою

Р (х ₁ < X < x ₂, y ₁ < Y < y ₂) = 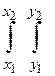j(x,y) dx dy. (9)

При нормальному розподілі системи двох випадкових величин отримаємо

Р (х ₁ <X<x ₂, y ₁ <Y<y ₂)=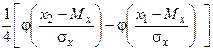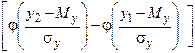. (10)

3. Числові характеристики системи двох випадкових величин. Кореляційний момент, коефіцієнт кореляції і рівняння регресії

Найбільш повними ймовірними характеристиками системи двох випадкових величин є закон розподілу. Однак в практичній діяльності не завжди є можливість визначити його. Тому при дослідженнях систему двох випадкових величин характеризують їх числовими характеристиками: початковими та центральними моментами.

Початковим моментом 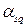порядку s, q системи (Х,Y) називається математичне сподівання від добутка Х^S на 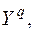тобто

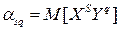. (11)

Для системи дискретних випадкових величин

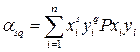, (12)

де Рx_iy_i = Р (Х = х_і; Y = y_i) - ймовірність того, що система (х,у) прийме значення (х_і, у_і),адодавання розповсюджується по всіх можливих значеннях випадкових величин Х і Y.

Дата добавления: 2014-01-04