Для системи неперервних випадкових величин

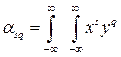j(х,у) dx dy, ( 13 )

де j(х,у)-щільність розподілу системи двох випадкових величин Х та Y.

В практичній діяльності найчастіше використовують початкові моменти першого порядку при s = 1, q = 0 і s = 0, q = 1

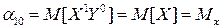; (14)

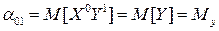. (15)

Як видно із формул (14) і (15) початковими моментами першого порядку будуть математичні сподівання випадкових величин Х і Y. Вони визначають координати точки, яку називають центром розсіювання системи (Х, Y)на площині.

Центральним моментом m _sqпорядку s, q системи (Х, Y) називається математичне сподівання добутку центрованих величин (Х – М_x) і (Y – M_y) відповідно в s-му і q-му степенях.

m _sq = М [(X – M_x) ^S (Y – M_y) ^q ]. (16)

Для системи дискретних і неперервних величин отримаємо:

m _sq = 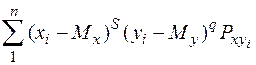; (17)

m _sq = 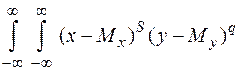j(х,у) dx dy. (18)

Практичне значення мають центральні моменти другого порядку при s = 2 і q = 0 та s = 0 і q = 2:

m₂₀ = М [(X – M_x)² (Y – M_y)⁰ ] = М [(X – M_x)²] = D_x; (19)

m₀₂ = М [(X – M_x)⁰ (Y – M_y)² ] = М [(Y – M_y)²] = D_y. (20)

Як видно вони є дисперсіями випадкових величин Х та Y і характеризують розсіювання випадкової точки з координатами (х, у) в напрямку осей 0 х і 0 y.

При дослідженнях системи випадкових величин важливу роль має змішаний центральний момент першого порядку - m₁₁. Його називають кореляційним моментом K_ху або моментом зв’язку і визначають за формулою

m₁₁ = K_ху = М [(X – M_x) (Y – M_y)].(21)

Для системи дискретних та неперервних величин його визначають за формулами

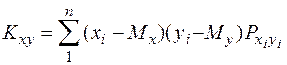; (22)

K_ху = 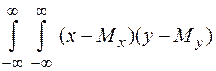j(х,у) dx dy. (23)

Між випадковими величинами Х і Y може виникати зв’язок. Кореляційний момент K_ху і характеризує силу або щільність зв’язку. Відомо, якщо між випадковими величинами існує ймовірний зв’язок (залежність), то зі зміною випадкової величини Х змінюється закон розподілу випадкової величини Y. В той же час закон розподілу задають кривою розподілу у = f (x). Характер кривих може бути різним, тому і відрізняють декілька типів імовірної залежності. Одним із найбільш розповсюджених типів є кореляційна залежність, за якої заміна аргументу х призводить до зміни математичного сподівання величини y (рис.3). В першому випадку (рис.3, а) ми маємо прямолінійну кореляцію, а на рис.3, б – криволінійну. При дослідженнях можуть виникнути й інші типи кореляційної залежності.

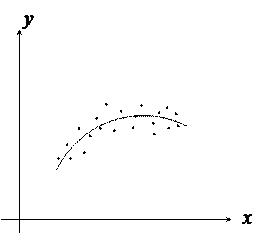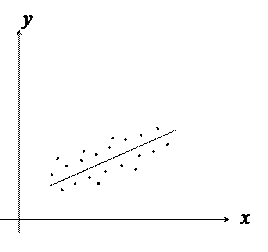а б

Рис.3

Кореляційну залежність часто називають кореляцією. Кореляційний момент має розмірність, яка залежить від розмірності випадкових величин Х і Y. Тому для оцінки сили зв’язку між випадковими величинами системи (Х, Y) використовують не коефіцієнт зв’язку K_ху, а безрозмірне відношення

, (24)

яке називають коефіцієнтом кореляції випадкових величин Х і Y. Коефіцієнт кореляції змінюється в межах від - 1 до +1, тобто

.

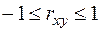Якщо r > 0, то маємо позитивну кореляцію, тобто із збільшенням абсциси x, збільшується величина ординати y (рис.3, а) і навпаки при r < 0.

Якщо випадкові величини Х і Y незалежні, то кореляційний момент і коефіцієнт кореляції дорівнює нулю, тобто K_ху = 0 і r_xy = 0.

Дві корельовані випадкові величини завжди є взаємозалежними, але дві залежні величини не завжди є корельованими.

Випадкові величини Х і Y називають корельованими, якщо | r_xy | > 0 і при r_xy = 0 – некорельованими.

Коли коефіцієнт кореляції дорівнює +1 чи - 1, то між величинами Х і Y існує прямолінійна залежність у вигляді рівняння прямої

у = ах + b.

Форма прямолінійного зв’язку між випадковими величинами Х і Y визначається у вигляді рівняння регресії Y на Х:

у = М_y + 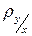(х – М_x), (25)

і Х на Y

x = М_x + 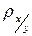(y – М_y). (26)

Коефіцієнти регресі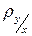ї і 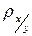визначають за формулами

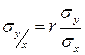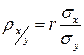; , (27)

де значення r, s _x, s _y обчислюють за відомими формулами.

4. Багатовимірний розподіл. Числові характеристики системи довільного числа випадкових величин

Якщо система включає більше двох величин, то її розглядають як випадкові точки або випадкові вектори в просторі відповідної кількості п -вимірів.

Повною характеристикою системи п -випадкових величин (Х ₁, Х ₂ ,..., Х_п) є закон розподілу цієї системи. Його задають функцією розподілу або щільністю розподілу.

Функцію п-аргументів х ₁, х ₂ ,..., х_п, що дорівнює ймовірності спільного виконання п-нерівностей Х_і < x_i (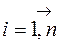) називають функцією розподілу системи (Х₁, Х₂,..., Х_п), тобто

F (х ₁, х ₂, …, х_п) = P (Х ₁ < x ₁, Х ₂ < x ₂, …, Х_n < x_n). (29)

Граничне відношення ймовірності появи системи (Х ₁, Х ₂ ,...,Х_п) в невеликих межах навколо точки (х ₁, х ₂, …, х_п) до розміру інтервалу межі при необмеженому його зменшенні називають щільністю розподілу j(х ₁, х ₂ ,..., х_п) системи п випадкових величин

j(х ₁, х ₂ ,..., х_п) = 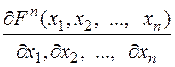. (30)

Якщо закон розподілу системи п- випадкових величин (Х ₁, Х ₂ ,..., Х_п)невідомий, то її характеризують числовими характеристиками:

1. Математичним сподіванням М_x

М_x = 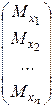, (31)

де 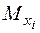– обчислюються за формулами..

2. Дисперсією D_x

D_x =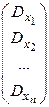. (32)

Дата добавления: 2014-01-04