Дисперсії характеризують міру точності кожної з випадкових величин, тобто розсіювання випадкової точки в напрямку осей

3. Кореляційною матрицею K_x

Вона є узагальненим поняттям дисперсії D_x для випадкового вектора Х. Визначається за формулою

K_x = М [(X – M_x) (X – M_x) ^T ]. (33)

Відомо, що математичне сподівання випадкової матриці є матриця, складена із математичних сподівань її елементів. У формулі (33) приймемо п = 3, отримаємо

K_x = = ,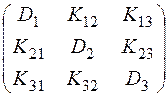

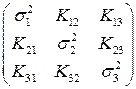де 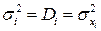– дисперсії Х_і, а K_ij = 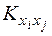– кореляційні моменти випадкових величин Х _і і Х_j.

При п- випадкових величинах системи (Х ₁, Х ₂ ,..., Х_п) кореляційна матриця має вигляд

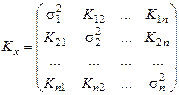. (34)

Аналіз формули (34) показує, що діагональні елементи кореляційної матриці 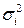є дисперсіями випадкових величин Х_і, а недіагональні елементи K_ij є кореляційними моментами між випадковими величинами Х_і і Х_j. Крім того, кореляційна матриця K_x симетрична відносно головної діагоналі, тобто

.

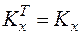Якщо випадкові величини системи (Х₁, Х₂,..., Х_п) незалежні між собою, то матриця K_x буде діагональною

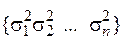= . (35)

Якщо всі дисперсії матриці (35) рівні між собою, 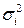= = 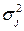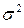то

K_x = s² E, (36)

де Е – одинична матриця.

Через кореляційні моменти K_ij можна обчислити коефіцієнти кореляції, що визначають міру зв’язку між парами Х_і і Х _j випадкових величин за формулою

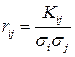. (37)

На заміну кореляційної матриці можна скласти нормовану кореляційну матрицю.

Нормованою кореляційною матрицею називають матрицю, елементами якої є коефіцієнти кореляції r_ij, тобто

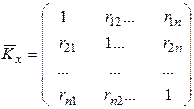. (38)

Якщо випадкові величини Х ₁, Х ₂ ,..., Х_п мають нормальний розподіл і незалежні між собою, то система випадкових величин (Х ₁, Х ₂ ,..., Х_п)буде п -вимірним нормальним розподілом зі щільністю ймовірності

j(х ₁ ,х ₂ ,..., х_п)= 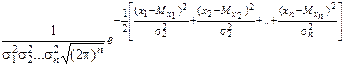. (39)

Щільність нормального розподілу для системи двох залежних величин Х і Y буде

j(х,у) =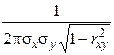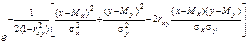. (40)

Як видно із формули (40), для двох залежних випадкових величин закон розподілу визначається п’ятьма параметрами: М_x, М_y, s _х, s _у і r_xy.

Формула щільності нормального розподілу для системи (Х ₁, Х ₂ ,..., Х_п)залежних випадкових величин Х ₁, Х ₂ ,..., Х_п має досить складний вигляд.

5. Функції випадкових величин. Числові характеристики. Кореляційна матриця системи функцій випадкових величин

В практиці геодезичних вимірювань виникають задачі оцінки точності результатів, що є функціями однієї чи декількох виміряних величин. Отримані функції теж будуть випадковими величинами. Як правило, відомо закон розподілу системи випадкових аргументів і відома функціональна залежність. Тобто, є система випадкових величин (Х ₁, Х ₂ ,..., Х_п) і законїх розподілу. Розглянемо функцію Y від випадкових величин Х ₁, Х ₂ ,..., Х_п

Y = f (Х ₁, Х ₂ ,..., Х_п). (41)

Практично вирішують задачу визначення закону розподілу випадкової величини Y, виходячи з функції (39) і закону сумісного розподілу її аргументів Х ₁, Х ₂ ,..., Х_п.

Покажемо вирішення цієї задачі для двох випадкових величин. Маємо функцію

Y = f (X ₁, X ₂).

Очевидно, що щільність розподілу системи випадкових величин (Х ₁, Х ₂) буде – j(x ₁, x ₂).

Штучно введемо нову величину Y ₁ = X ₁ і розглянемо систему двох рівнянь

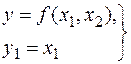. (42)

Очевидно, цю систему можна однозначно визначити відносно х ₁та х ₂, тоді

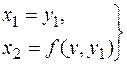. (43)

Виходячи з того, що система (3.43) диференціюється в теорії ймовірностей, доводиться, що щільність розподілу випадкової величини

у = f (x ₁, x ₂) в нескінченних межах буде

j(у) = 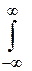j[ x ₁j y,x ₁)]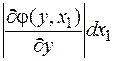. (44)

За аналогією находять щільність розподілу для функції трьох і більше випадкових величин. Наприклад, якщо Y = f (x ₁, x ₂, x ₃), вводять нові перемінні

Y ₁ = X ₁,

Y ₂ = X _2.

Якщо при цьому між системами (Х ₁, Х ₂, Х ₃)і (Y, Y ₁, Y ₂)виявляється однозначне співвідношення, то щільність розподілу випадкової величини Y буде

j(у) = 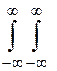j[ x ₁, х ₂, j(y,x ₁, х ₂)]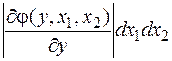, (45)

де j(y, x ₁, x ₂) – зворотня функція.

На основі формули (44) визначають щільність розподілу для випадкових величин: у = (x ₁ + x ₂); у = (x ₁ - x ₂); у = x ₁ × x ₂ та 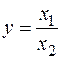Наприклад. Закон розподілу величини відхилення випадкової точки (Х,Y) від початку координат при умові, що система випадкових величин (Х, Y) має нормальний розподіл з параметрами М_х = М_y = 0 і s _х = s _у = s називають розподілом Релея.

Зазначимо, що щільність розподілу такої системи (Х, Y) має вигляд

j(х,у) = .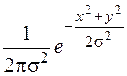

Відхилення точки (х,у ) від початкукоординат буде визначатися випадковим вектором R, що є функцією випадкових величин Х та Y, тобто

.

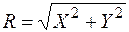Випадкова величини R є полярним радіусом, тоді

x = r cos q;

y = r sin q.

Щільність розподілу j(r,q)системи випадкових величин (R, q)визначають через щільність розподілу j(х, у)системи (Х, Y).

Внаслідок математичних перетворень щільність розподілу випадкової величини R визначається розподілом Релея за формулою

j(r) = 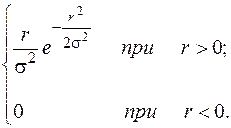. (46)

Графік розподілу Релея показано на рис. 4

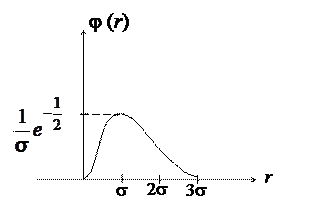Рис. 4

При дослідженнях не завжди виникає необхідність у визначенні закону розподілу функції випадкових величин. Тоді обчислюють числові характеристики функції випадкових величин: математичне сподівання та дисперсію.

Дата добавления: 2014-01-04