
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
При растяжении и сжатии бруса меняются его продольные и
|
|
|
|
ДЕФОРМАЦИИ И ПЕРЕМЕЩЕНИЯ ПРИ
РАСТЯЖЕНИИ — СЖАТИИ
поперечные размеры (рис. 3.5).
При растяжении длина бруса меняется на:
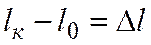 ,
,
а ширина бруса меняется на:
 .
.
При сжатии:
 ,
, 
где 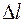 — абсолютная продольная деформация (см, м);
— абсолютная продольная деформация (см, м);
 — абсолютная поперечная деформация (см, м).
— абсолютная поперечная деформация (см, м).


Рис. 3.5
Перейдем к относительным деформациям (безразмерным):
 - относительная продольная деформация;
- относительная продольная деформация;
 - относительная поперечная деформация.
- относительная поперечная деформация.
При растяжении бруса
 ;
;
при сжатии
 ,
,
т. е. и при растяжении, и при сжатии 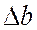 и
и 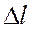 , а следовательно,
, а следовательно,  и
и 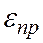 имеют разные знаки, поэтому отношение этих величин (всегда отрицательное) берется по абсолютной величине.
имеют разные знаки, поэтому отношение этих величин (всегда отрицательное) берется по абсолютной величине.
Коэффициент поперечной деформации, или коэффициент Пуассона (табл. 3.1):
 . (3.4)
. (3.4)
Таблица 3.1
| Материал | 
|
| Сталь легированная Чугун серый | 0,25 – 0,3 0,23 — 0,27 |
Закон Гука выражает прямо пропорциональную зависимость между нормальным напряжением и относительной деформацией:
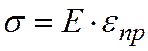 . (3.5)
. (3.5)
Закона Гука можно представить в другом виде:
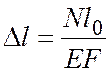 . (3.6)
. (3.6)
Из последнего выражения легко получить выражение (3.5):
 ,
,
где E —модуль продольной упругости (физическая постоянная материала, характеризующая его способность сопротивляться упругому деформированию, табл. 2);
EF —жесткость поперечного сечения бруса при растяжении — сжатии.
Таблица 3.2
| Материал | 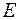 , МПа , МПа
|
| Сталь легированная Чугун серый Стекло Медь прокатная Алюминиевая проволока | (2,1 — 2,2) • 105 (1,15 —1,6) • 105 0,56 105 1,10 105 0,70 105 |
Деформация бруса (растяжение или сжатие) вызывает перемещение поперечных сечений. На рис. 3.6 показан брус, каждое волокно которого удлиняется на величину
 - (здесь
- (здесь 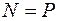 ),
),
а сечение 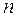 —
— 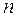 перемещается в положение
перемещается в положение  —
—  на величину
на величину  .
.


Рис. 3.6 Рис. 3.7
В этом случае:
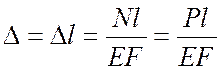 .
.
Рассмотрим брус, показанный на рис. 3.7. Левый участок бруса деформируется и сечение 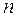 —
— 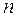 перемещается в положение
перемещается в положение  —
—  на величину
на величину  ; правый участок не деформируется (нет продольной силы) и каждое его сечение оказывается перемещенным на эту же величину
; правый участок не деформируется (нет продольной силы) и каждое его сечение оказывается перемещенным на эту же величину  . Сечение т — т переместится на столько же, насколько переместилось сечение
. Сечение т — т переместится на столько же, насколько переместилось сечение 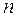 —
— 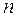 :
:
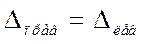 .
.
Рассмотрим случай, когда продольная сила есть на обоих участках рассматриваемого бруса (рис. 3.8). Перемещение сечения т — т ( ) (правое сечение) зависит от перемещения сечения
) (правое сечение) зависит от перемещения сечения 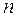 —
— 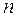 (
( ) и перемещения сечения т — т относительно сечения п — п (
) и перемещения сечения т — т относительно сечения п — п (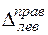 ):
):
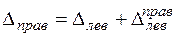 ,
,
где  .
.
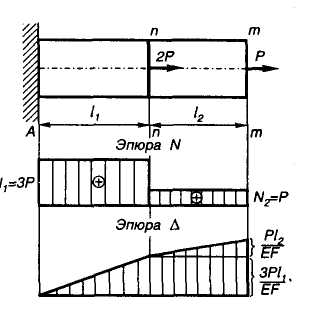
Рис. 3.8
Для рассматриваемого примера (EF= const):
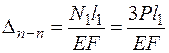 ;
;
 .
.
Перемещение  можно получить, используя не внутренние усилия
можно получить, используя не внутренние усилия 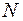 , а внешние силы. Рассуждаем так: сила
, а внешние силы. Рассуждаем так: сила  растягивает только участок длиной
растягивает только участок длиной  сила
сила  растягивает весь брус длиной
растягивает весь брус длиной  :
:
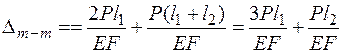 .
.
Используя полученные значения, построим эпюру перемещений (рис. 3.8). Учитываем, что в заделке перемещение равно нулю ( ).
).
При перемещении бруса от действия собственного веса (рис. 3.9), считая вес груза сосредоточенным в середине длины  , получим
, получим
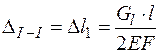 ,
,

Рис. 3.9
где  — вес бруса длиной
— вес бруса длиной  ;
;  — удельный вес материала.
— удельный вес материала.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 447; Нарушение авторских прав?; Мы поможем в написании вашей работы!