Построение разверток призматических и цилиндрических поверхностей

ЛЕКЦИЯ №17

Цилиндрическая поверхность, как и призматическая вписанная (или описанная) в цилиндрическую поверхность и заменяющая её, состоит из параллелограммов. Натуральный вид параллелограммов можно построить двумя способами:

· либо по высоте и длине противоположных сторон;

· либо способом триангуляции, разбив параллелограмм на два треугольника.

Построение параллелограммов по их основаниям и высоте проще. В этом случае необходимо определить высоты и отрезки оснований, на которые их делит высота.

Для определения высот параллелограммов при построении развёрток призматических и цилиндрических поверхностей строят натуральный вид «нормального» сечения этих поверхностей. Если поверхность призматическая, то высотами являются стороны нормального сечения, а если цилиндрическая - хорды, стягивающие дуги «нормального» сечения на которые разделена кривая, ограничивающая это сечение. Такой способ построения развёрток называется способом «нормального» сечения.

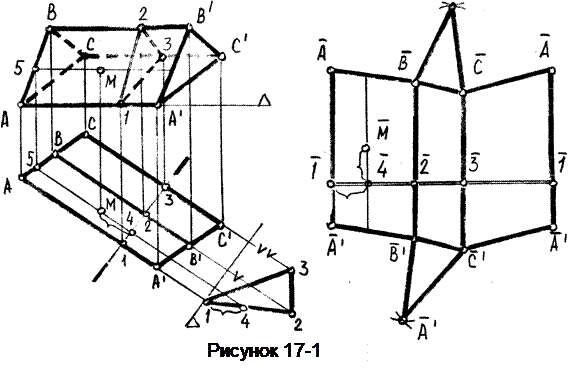Пример 1. Построить полную развёртку поверхности треугольной призмы (рисунок 17-1) и нанести на ней точку М, принадлежащую поверхности.

Призма расположена таким образом, что её боковые ребра являются горизонталями, следовательно на виде сверху они имеют натуральную величину.

Чтобы построить «нормальное» сечение проведём вертикальную плоскость Б перпендикулярно к боковым ребрам призмы. Построим натуру сечения с помощью дополнительного вида, выполненного по направлению горизонтали, перпендикулярной к плоскости Б. Стороны треугольника натурального вида сечения будут являться искомыми высотами параллелограммов.

Т.к. при построении развёртки углы и параллельности сохраняются, то на развёртке боковые ребра будут параллельны между собой и перпендикулярны прямой линии, в которую развернётся «нормальное» сечение.

Построение развёртки начинается с проведения прямой линии, на которой откладываем длины сторон нормального сечения (высоты параллелограммов) 1-2, 2-3, 3-1.

Через концы этих сторон проведём прямые перпендикулярные им. На полученных перпендикулярах отложим отрезки боковых рёбер, измеренные на виде сверху относительно нормального сечения. Соединив между собой полученные точки отрезками прямых, получим развёртку боковой поверхности призмы. Присоединив к этой развёртке оба основания, получим полную развёртку поверхности призмы.

Чтобы построить на развёртке точку М, принадлежащую поверхности призмы, необходимо найти на развёртке положение прямой, на которой эта точка лежит. Для этого найдём точку пересечения этой прямой с плоскостью Б на натуральном виде сечения. Замерим расстояние 1-4 и отложим его на развёртке. Через полученную точку проведём прямую, параллельную ребрам призмы. Затем измерим на виде сверху длину отрезка - от нормального сечения до точки М и отложим его на развёртке.

Пример 5. Построить развёртку боковой поверхности эллиптического цилиндра и нанести на неё точку М, принадлежащую поверхности цилиндра (рисунок 17-2).

Для построения развертки заменяем цилиндрическую поверхность вписанной призматической поверхностью.

Перпендикулярно образующим цилиндра проводим наклонную плоскость Б.

С помощью дополнительного вида, построенного по направле­нию фронтали, определяем натуральный вид «нормального» сечения.

Так как цилиндрическая поверхность имеет фронтальную плоскость симметрии, то построим развёртку только половины поверхности. Часть полуэллипса («нормальное» сечение будет эллипсом) разделим на шесть частей таким образом, чтобы стягивающие эти части хорды, возможно меньше отличались от дуг. Через точки деления проводим на поверхности цилиндра образующие. Таким образом половина поверхности цилиндра будет разбита на шесть параллелограммов.

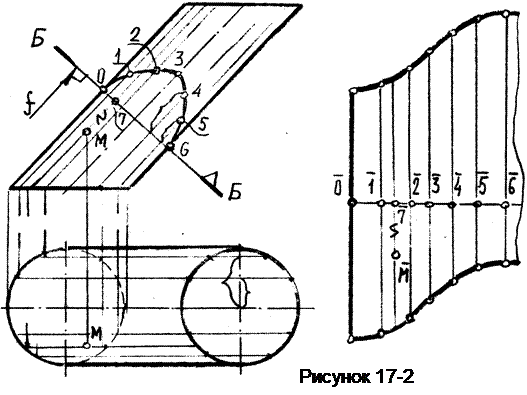Строим прямую линию, в которую развернётся «нормальное» сечение, и на ней откладываем длины хорд, стягивающих «нормальное» сечение. Через концы отложенных хорд (являющихся высотами параллелограммов) проводим перпендикулярные к ним прямые. Затем замеряем на виде спереди части образующих цилиндра, относительно нормального сечения и откладываем их на развёртке. Концы образующих соединяем плавной кривой.

Чтобы построить на развёртке точку М, наносим сначала на ней положение образующей, на которой эта точка лежит. Для этого измерим на натуральном виде нормального сечения хорду от точки 1 до точки 7, в которой эта образующая пересекается с плоскостью Б, и отложим её на развёртке. На проведённой через полученную точку 7 образующей откладываем отрезок, измеренный на виде спереди от нормального сечения до точки М.

Дата добавления: 2014-01-04