Включение RC-цепи на постоянное напряжение

Напряжение на емкостном элементе в начальный момент времени после коммутации имеет то же значение, которое оно имело непосредственно перед коммутацией, а затем с этого значения он начинает плавно изменятся.

Ток в ветви с индуктивным элементом в начальный момент времени после коммутации имеет то же значение, которое он имел непосредственно перед коммутацией, а затем с этого значения он начинает плавно изменятся.

iL(0_)=iL(0)

(1)

Где: i_L(0_) – мгновенное значение тока до коммутации;

I_L(0) – мгновенное значение тока после коммутации.

uC(0_)=uC(0)

(2)

Пример расчета переходного процесса при последовательном соединении R,L,C при подключению к источнику периодически изменяющейся эдс. (рис.1).

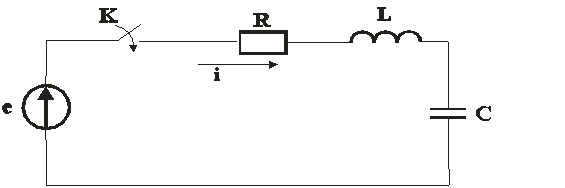
Рисунок 1. Схема электрической цепи.

Электрическое состояние цепи после коммутации, согласно второму закону Кирхгофа описывается уравнением:

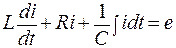
(3)

Для этой цепи переходный процесс описывается уравнением второго порядка, так как значения i и u можно задать независимо друг от друга:

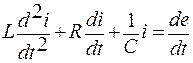
(4)

Решение уравнения представляет собой сумму двух решений: частного неоднородного и общего решения однородного уравнения. Частное решение описывает принужденный режим, задаваемый источником энергии. Общее решение описывает переходный процесс, протекающий за счет энергии накопленной в индуктивных и емкостных элементах цепи до начала процесса. При отсутствии внешнего источника энергия, запасенная в цепи, постепенно расходуется и снижается до нуля.

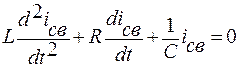
(5)

Характеристическое уравнение:

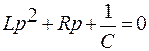
(6)

Корни характеристического уравнения

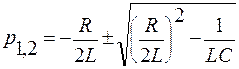
(7)

В зависимости от значения корней уравнений получены частные решения дифференциального уравнения свободного тока.

1.Если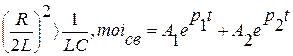

(8)

2.Если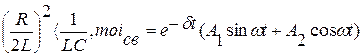

(9)

3.Если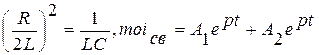

(10)

Где А₁ и А₂ постоянные интегрирования, р₁ и р₂ – корни характеристического уравнения.

Для 2 случая корни равны:

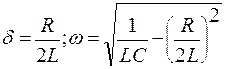
(11)

Действительное значение тока равно сумме принужденного и свободного токов: i=i_пр+i_св

ПРИМЕРЫ:

1.Включение RL –цепи на постоянное напряжение.

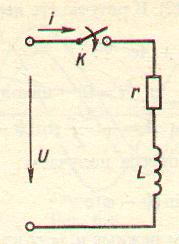
Рисунок 2. Схема цепи.

При включении RL – цепи на постоянное напряжение U=U₀, принужденный ток 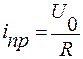, а свободный ток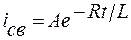

Тогда ток переходного процесса:

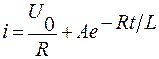
(12)

Так как ток до переходного процесса и в первый момент времени равен нулю, отсюда 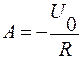. В результате искомый переходный ток:

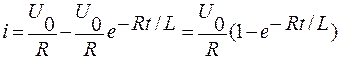
(13)

Напряжение на индуктивном элементе:

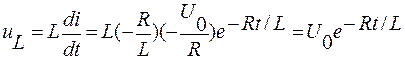
(14)

Напряжение на резистивном элементе:

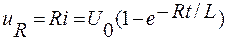
(15)

До коммутации напряжение на индуктивном элементе было равно нулю, а в момент включение. В первый момент включения напряжение целиком сосредоточивается только на индуктивном элементе, а затем постепенно переходит на резистивный элемент.

Ток в цепи не устанавливается мгновенно, для него требуется определенное время. Возрастание переходного тока будет медленнее, чем больше постоянная времени τ=L/R. На рисунке 3 приведены графики изменения токов и напряжений при переходном процессе.

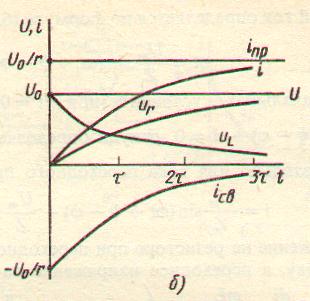
Рисунок 3. График изменения токов и напряжений при переходном процессе.

При включении этой цепи конденсатор будет заряжаться до определенного напряжения u_C=U₀ рисунок 1.

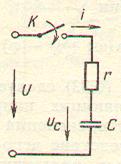
Рисунок4 Схема RC при включении на постоянное напряжение.

Тогда свободное напряжение на емкостном элементе будет равно:

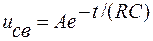
(16)

Тогда переходное напряжение на емкостном элементе:

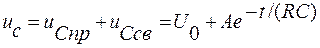
(17)

Напряжение на емкостном элементе до коммутации, а следовательно, и в первый момент включения равно нулю, так как конденсатор не был заряжен, отсюда следует, что переходное напряжение будет равно:

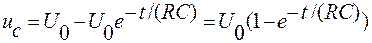
(18)

Из этого следует, что напряжение на конденсаторе возрастает постепенно, причем тем медленнее, чем больше постоянная времени τ=RC.

Ток при зарядке конденсатора в момент коммутации возникает скачком, а затем спадает по экспоненциальному закону. Ток спадает тем медленнее, чем больше постоянная времени, и находится по формуле:

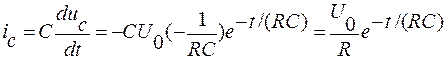
(19)

На рисунке 5 изображены графики тока и напряжения при зарядке конденсатора.

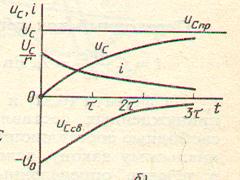
Рисунок 5. Графики тока и напряжения при зарядке конденсатора.

Дата добавления: 2014-01-04