
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нормальные подгруппы
|
|
|
|
Определение 3.4.1. Пусть H – подгруппа группы G и 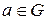 . Обозначим aH множество элементов { a · h | h Î H } и назовем его левым смежным классом группы G по подгруппе H. Элемент a называется представителем левого смежного класса aH.
. Обозначим aH множество элементов { a · h | h Î H } и назовем его левым смежным классом группы G по подгруппе H. Элемент a называется представителем левого смежного класса aH.
Если существует 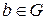 , b Ï H È aH, то можно построить левый смежный класс bH и т.д.
, b Ï H È aH, то можно построить левый смежный класс bH и т.д.
Аналогично строятся правые смежные классы Ha = { h · a | h Î H } с представителями 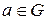 .
.
Теорема 3.4.1. Пусть H – подгруппа группы G. Тогда
1) каждый элемент  принадлежит какому-нибудь левому (правому) смежному классу по подгруппе H;
принадлежит какому-нибудь левому (правому) смежному классу по подгруппе H;
2) два элемента  принадлежат одному левому (правому) смежному классу тогда и только тогда, когда a –1· b Î H (b · a –1 Î H);
принадлежат одному левому (правому) смежному классу тогда и только тогда, когда a –1· b Î H (b · a –1 Î H);
3) любые два левых (правых) смежных класса либо не пересекаются, либо совпадают;
4) G есть объединение попарно непересекающихся левых (правых) смежных классов по подгруппе H.
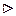 1) Для "
1) Для " g = g · e, так как e Î H, то g Î { g · h | h Î H } = gH. Аналогично g = e · g Þ g Î { h · g | h Î H } = Hg.
g = g · e, так как e Î H, то g Î { g · h | h Î H } = gH. Аналогично g = e · g Þ g Î { h · g | h Î H } = Hg.
2) a Î aH, b Î bH. a и b принадлежат одному и тому же левому смежному классу Û $ h Î H такой, что b = a · h, Û a –1· b = h Û a –1· b Î H.
a Î Ha, b Î Hb. a и b принадлежат одному и тому же правому смежному классу Û $ h Î H такой, что b = h · a, Û b · a –1 = h Û b · a –1 Î H.
3) Пусть c Î aH Ç bH Û для некоторых h 1, h 2 Î H c = a · h 1 = b · h 2 Û b –1· a = h 2· h 1–1 Î H Û a, b принадлежат одному и тому же левому смежному классу согласно утверждению 2, то есть aH = bH.
Пусть c Î Ha Ç Hb Û c = h 1· a = h 2· b Û a · b –1 = h 1–1· h 2 Î H Û Ha = Hb.
Либо aH Ç bH = Æ (Ha Ç Hb = Æ).
4) Следует из утверждений 1 и 3.
Определение 3.4.2. Мощность множества всех различных левых (правых) смежных классов группы G по подгруппе H называется индексом подгруппы H в группе G и обозначается G: H.
К важнейшим в теории групп относится следующая теорема, доказанная известным французским математиком и механиком Жозефом Лагранжем (1736–1813).
Теорема 3.4.2 (Ж. Лагранж). Порядок конечной группы равен произведению порядка и индекса любой ее подгруппы.
 Пусть H £ G, | G | = n, | H | = k, n, k Î N, и H = { e = h 1, h 2,…, hk }.
Пусть H £ G, | G | = n, | H | = k, n, k Î N, и H = { e = h 1, h 2,…, hk }.
Для " a Î G aH = { a, a · h 2,…, a · hk }, Ha = { a, h 2· a,…, hk · a }. Покажем, что | H | = | aH | = | Ha |. Действительно, a · hi = a · hj Û a –1·(a · hi) = a –1·(a · hj) Û hi = hj, аналогично hi · a = hj · a Û hi = hj для всех  . В общем случае, даже для бесконечной подгруппы H, H «aH «Ha.
. В общем случае, даже для бесконечной подгруппы H, H «aH «Ha.
Согласно утверждению 4 теоремы 3.4.1 G есть объединение попарно непересекающихся левых (правых) смежных классов по подгруппе H. Таким образом,  (объединение всех различных смежных классов) Þ | G | = | H | × (G: H) и G: H = n / k.
(объединение всех различных смежных классов) Þ | G | = | H | × (G: H) и G: H = n / k. 
Следствие 1. Порядок конечной группы делится на порядок любой ее подгруппы.
Следствие 2. Если G – конечная группа порядка n, то порядок любого элемента группы делит порядок группы и для каждого 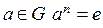 .
.
 Пусть | G | = n. Рассмотрим < a > для " a Î G, очевидно, что ord (a) £ n. | < a > | = ord (a) согласно теореме 3.3.3. < a > £ G, значит, по следствию 1 из теоремы 3.4.2 ord (a) | n. Отсюда следует, что
Пусть | G | = n. Рассмотрим < a > для " a Î G, очевидно, что ord (a) £ n. | < a > | = ord (a) согласно теореме 3.3.3. < a > £ G, значит, по следствию 1 из теоремы 3.4.2 ord (a) | n. Отсюда следует, что 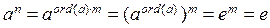 , где
, где  .
.
Следствие 3. Любая группа простого порядка является циклической и не содержит собственных подгрупп.
 Пусть порядок группы G | G | = p – простое число. Рассмотрим " a Î G \{ e }. Согласно следствию 1 из теоремы 3.4.2 | < a > | | p, откуда | < a > | = 1 или | < a > | = p. Но в первом случае < a > = < e > и a = e, что не так. Поэтому | < a > | = p, значит, G = < a >.
Пусть порядок группы G | G | = p – простое число. Рассмотрим " a Î G \{ e }. Согласно следствию 1 из теоремы 3.4.2 | < a > | | p, откуда | < a > | = 1 или | < a > | = p. Но в первом случае < a > = < e > и a = e, что не так. Поэтому | < a > | = p, значит, G = < a >.
По следствию 1 из теоремы 3.4.2 порядок любой подгруппы H в G равен 1 или p, то есть H = { e } или H = G. 
Так как для произвольной группы (G, ·) и " a Î G, следуя доказательству теоремы 3.4.2, G «aG «Ga, то aG = G = Ga и G: G = 1.
Пример 3.4.1. Рассмотрим (n Z, +) £ (Z, +) для " n Î N и найдем все смежные классы Z по n Z. Поскольку (Z, +) – абелева группа, то для одинаковых представителей левые смежные классы совпадают с соответствующими правыми. Таким образом, для " z Î Z z = nq + r, где q, r Î Z, 0 £ r < n, согласно теореме 1.1.1, и z + n Z = n Z + z = { nm + r | m Î Z } = 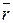 в Z/ n Z. В частности n Z =
в Z/ n Z. В частности n Z = 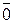 в Z/ n Z. Итак,
в Z/ n Z. Итак,  = Z/ n Z – множество всех различных левых (правых) смежных классов группы (Z, +) по подгруппе (n Z, +). Значит, Z: n Z = n.
= Z/ n Z – множество всех различных левых (правых) смежных классов группы (Z, +) по подгруппе (n Z, +). Значит, Z: n Z = n.
Здесь (Z, +) – бесконечная группа, (n Z, +) – ее бесконечная подгруппа, а индекс Z: n Z конечен. ·
Пример 3.4.2. (V 4(Z /2 Z), +) – аддитивная группа всех строк-векторов с четырьмя координатами из Z /2 Z. Рассмотрим следующее подмножество в V 4(Z /2 Z): 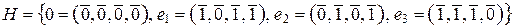 . Легко проверить, что H < V 4(Z /2 Z). | V 4(Z /2 Z) | = 24 = 16, | H | = 4, значит, V 4(Z /2 Z): H = 16: 4 = 4. Для одинаковых представителей левые смежные классы совпадают с правыми, поскольку (V 4(Z /2 Z), +) – абелева группа.
. Легко проверить, что H < V 4(Z /2 Z). | V 4(Z /2 Z) | = 24 = 16, | H | = 4, значит, V 4(Z /2 Z): H = 16: 4 = 4. Для одинаковых представителей левые смежные классы совпадают с правыми, поскольку (V 4(Z /2 Z), +) – абелева группа.
Выпишем таблицу 3.4.1 смежных классов группы (V 4(Z /2 Z), +) по подгруппе (H, +).
Таблица 3.4.1
| № | класс a + H | a + 0 | a + e 1 | a + e 2 | a + e 3 |
| 1. | 0 + H = H | 
| 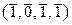
| 
| 
|
| 2. | 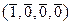 + H + H
| 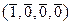
| 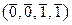
| 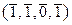
| 
|
| 3. | 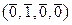 + H + H
| 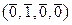
| 
| 
| 
|
| 4. |  + H + H
| 
| 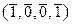
| 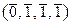
| 
|
·
Определение 3.4.3. Подгруппа H группы G называется нормальной, если для всякого 
 , то есть каждый левый смежный класс по подгруппе H совпадает с правым смежным классом с тем же представителем. В этом случае используется обозначение: H
, то есть каждый левый смежный класс по подгруппе H совпадает с правым смежным классом с тем же представителем. В этом случае используется обозначение: H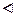 G.
G.
Ясно, что у абелевых групп все подгруппы нормальны.
В любой группе (G, ·) тривиальные подгруппы { e } и G являются нормальными, так как для " a Î G a { e } = { a } = { e } a и aG = G = Ga. Итак, { e } 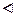 G и G
G и G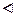 G.
G.
Пример 3.4.3. Если G: H = 2, то H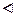 G для произвольной группы (G, ·). Поскольку для " g Î G \ H H Ç gH = H Ç Hg = Æ и G = H È gH = H È Hg согласно утверждениям 3 и 4 теоремы 3.4.1, Þ gH = Hg и, таким образом, aH = Ha для " a Î G. ·
G для произвольной группы (G, ·). Поскольку для " g Î G \ H H Ç gH = H Ç Hg = Æ и G = H È gH = H È Hg согласно утверждениям 3 и 4 теоремы 3.4.1, Þ gH = Hg и, таким образом, aH = Ha для " a Î G. ·
Теорема 3.4.3 (критерий нормальной подгруппы). H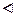 G тогда и только тогда, когда для каждого
G тогда и только тогда, когда для каждого 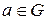
 (для " a Î G, " h Î H a · h · a –1 Î H).
(для " a Î G, " h Î H a · h · a –1 Î H).
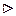 Необходимость. Пусть H
Необходимость. Пусть H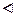 G, тогда для
G, тогда для 
 . Значит, для " h Î H $ h 1 Î H такой, что a · h = h 1· a, Û a · h · a –1 = h 1 Î H. Таким образом, для " a Î G aHa –1 = { a · h · a –1 | h Î H } Í H. Поскольку для всех hi, hj Î H справедливо a · hi · a –1 = a · hj · a –1 Û a –1·(a · hi · a –1)· a = a –1·(a · hj · a –1)· a Û hi = hj, то | aHa –1 | = | H | и aHa –1 = H.
. Значит, для " h Î H $ h 1 Î H такой, что a · h = h 1· a, Û a · h · a –1 = h 1 Î H. Таким образом, для " a Î G aHa –1 = { a · h · a –1 | h Î H } Í H. Поскольку для всех hi, hj Î H справедливо a · hi · a –1 = a · hj · a –1 Û a –1·(a · hi · a –1)· a = a –1·(a · hj · a –1)· a Û hi = hj, то | aHa –1 | = | H | и aHa –1 = H.
Достаточность. Пусть для " a Î G, " h Î H a · h · a –1 Î H (aHa –1 = H). Докажем, что aH Í Ha и Ha Í aH. Для " b Î aH $ h 1 Î H такой, что b = a · h 1, Û b · a –1 = a · h 1· a –1 Î H Þ $ h 2 Î H такой, что b = h 2· a Î Ha. Значит, aH Í Ha. Для " c Î Ha $ h 3 Î H такой, что c = h 3· a, Û a –1· c = a –1· h 3· a Î H Þ $ h 4 Î H такой, что c = a · h 4 Î aH. Значит, Ha Í aH. Итак, aH Í Ha и Ha Í aH, следовательно, aH = Ha для " a Î G и H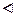 G.
G. 
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 731; Нарушение авторских прав?; Мы поможем в написании вашей работы!