
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 3.3.6
|
|
|
|
1. Для " z Î Z \{0} ord (z) = ¥ в (Z, +), поскольку при " n Î N n × z ¹ 0.
2. Для всех 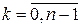 ord (
ord (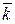 ) = ord (
) = ord (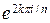 ) = n /(k, n) в (Z / n Z, +) и в Cn. ·
) = n /(k, n) в (Z / n Z, +) и в Cn. ·
Теорема 3.3.3. Пусть элемент a Î G обладает свойством: ord (a) = n для некоторого n Î N. Тогда < a > = {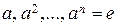 } – циклическая подгруппа группы G, имеющая порядок n.
} – циклическая подгруппа группы G, имеющая порядок n.
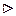 Пусть H = {
Пусть H = {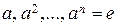 }, тогда | H | = n, так как ord (a) = n.
}, тогда | H | = n, так как ord (a) = n.
< a > = {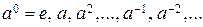 } = { az | z Î Z }. Очевидно, H Í < a >.
} = { az | z Î Z }. Очевидно, H Í < a >.
Рассмотрим " z Î Z. Если  , то az Î H. Если
, то az Î H. Если 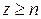 или
или  , то по теореме 1.1.1 существуют такие q, r Î Z, где
, то по теореме 1.1.1 существуют такие q, r Î Z, где  , что
, что 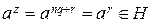 , поскольку
, поскольку  . Значит, < a > Í H.
. Значит, < a > Í H.
Итак, H = < a > – циклическая подгруппа, порожденная элементом a. 
Теорема 3.3.4. Всякая подгруппа H циклической группы G является циклической.
 Пусть G = < a >.
Пусть G = < a >.
1. H = { e } Þ H = < e >.
2. H ¹ { e }. Для " b Î H $ m Î Z такой, что b = am, так как H £ G и G = < a >. Поскольку H £ G, a – m Î H. Таким образом, в H содержатся некоторые степени элемента a с натуральными показателями. Из всех таких показателей выберем наименьший. Пусть это будет d Î N. Докажем, что H = < ad >.
< ad > Í H, так как ad Î H, и поскольку H £ G, то adz Î H для " z Î Z.
Рассмотрим теперь " h Î H. h = as = adq + r, где q, r Î Z, 0 £ r < d, согласно теореме 1.1.1, поскольку s Î Z. Тогда ar = a – dq · h Î H, так как a – dq, h Î H. Если r ¹ 0, то r < d и степень элемента a с меньшим натуральным показателем, чем d, принадлежит H, что приводит к противоречию. Значит, r = 0 и для некоторого q Î Z h = adq Î < ad >. Поэтому H Í < ad >.
Итак, H = < ad > – циклическая подгруппа группы G. 
Обозначим En единичную квадратную матрицу порядка n Î N.
Пример 3.3.7. Рассмотрим матрицу 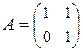 Î SL 2(Z). Здесь
Î SL 2(Z). Здесь 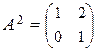 ,
,  ,…, таким образом,
,…, таким образом,  при " n Î N. Степени матрицы A попарно различны и образуют бесконечную последовательность. Следовательно, ord (A) = ¥ и циклическая подгруппа < A > = { Az | z Î Z }, порожденная матрицей A, в группе SL 2(Z) является бесконечной.
при " n Î N. Степени матрицы A попарно различны и образуют бесконечную последовательность. Следовательно, ord (A) = ¥ и циклическая подгруппа < A > = { Az | z Î Z }, порожденная матрицей A, в группе SL 2(Z) является бесконечной.
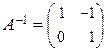 ,
,  ,…,
,…, 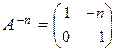 для " n Î N. Таким образом,
для " n Î N. Таким образом, 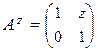 при " z Î Z. ·
при " z Î Z. ·
Пример 3.3.8. Матрица  Î SL 2(Z) имеет степени
Î SL 2(Z) имеет степени  ,
, 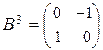 ,
,  . Поэтому ord (B) = 4 в группе SL 2(Z). Согласно теореме 3.3.3 подгруппа < B > = { B, B 2, B 3, B 4 = E 2} является конечной подгруппой порядка 4 в группе SL 2(Z). ·
. Поэтому ord (B) = 4 в группе SL 2(Z). Согласно теореме 3.3.3 подгруппа < B > = { B, B 2, B 3, B 4 = E 2} является конечной подгруппой порядка 4 в группе SL 2(Z). ·
Отметим, что чаще группы не являются циклическими. Например, все некоммутативные группы не могут быть циклическими. Циклическими не являются группы, заданные на несчетных множествах, например, (R, +), (C, +), (R *, ×) и (C *, ×).
Пример 3.3.9. Несмотря на то, что Q * «Q «Z, абелевы группы (Q, +) и (Q *, ×) также не цикличны. Ведь для каждого фиксированного q = m / n Î Q *, где m Î Z, n Î N, (m, n) = 1, подгруппа < q > = {0, ± m / n, ± 2 m / n, ± 3 m / n,…} не содержит рациональных несократимых дробей r / s при  Î Z, s Î N > n, следовательно, < q > ¹ Q. А подгруппа < q > = {1, (m / n)± 1, (m / n)± 2, (m / n)± 3,…} не содержит r / s Î Q *, где
Î Z, s Î N > n, следовательно, < q > ¹ Q. А подгруппа < q > = {1, (m / n)± 1, (m / n)± 2, (m / n)± 3,…} не содержит r / s Î Q *, где  Î Z, s Î N >1, (r, s) = 1 и (s, n) = (s, m) = 1, следовательно, < q > ¹ Q *. ·
Î Z, s Î N >1, (r, s) = 1 и (s, n) = (s, m) = 1, следовательно, < q > ¹ Q *. ·
§3.4. Смежные классы. Теорема Лагранжа.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 356; Нарушение авторских прав?; Мы поможем в написании вашей работы!