Первоначальная модель Нисканена

Уильям Нисканен впервые подошел к исследованию деятельности бюрократических учреждений с позиции анализа «издержек-выгод», по аналогии с тем, как неоклассика подходит к изучению деятельности фирмы. В центре внимания оказались традиционные вопросы: каков объем выпускаемой продукции, каковы издержки производства, как затраты и выпуск меняются с изменением условий. Применительно к фирме это означает соотношение затрат и выпуска.

Становление концепции Нисканена прошло два этапа. Ее первоначальный вариант был предложен в книге 1971 г. «Бюрократия и представительное правление». Суть концепции заключается в том, что бюро – организация, поставляющая данный объем общественных благ для монопольного покупателя своих услуг – обычно это группа политических должностных лиц (спонсор). В свою очередь бюро – тоже монополист (монопольный поставщик своих услуг). Возникает ситуация двухсторонней монополии, особенностью которой является обмен обещанной продукции на бюджет, который выделяется для бюро. Как в ситуации любой двухсторонней монополии, здесь нет единственного равновесия.

Предпочтения спонсора выражены функцией «бюджет - выпуск». В определенном интервале ожидаемого выпуска спонсор готов предоставить больший бюджет за больший ожидаемый выпуск:

B = aQ – bQ² , 0<Q<a/2b, (1)

Q – ожидаемый выпуск бюро;

B - максимальный бюждет, который спонсор готов предоставить бюро.

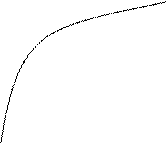
Предполагается, что B`>0 и B``<0. Эта функция представлена на рисунке 1.

Производная функции «бюджет-выпуск» не имеет операционного значения, так как бюро не предлагает отдельные услуги по отдельной цене. Она имеет определенный интерес для спонсора в том смысле, что аналогичные услуги могли поставляться конкурентной отраслью. Функция предельной полезности имеет вид

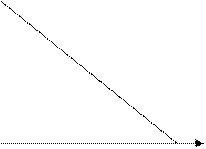
V = a – 2bQ, 0<Q<a/2b (2)

V    

B

где V – максимальная цена за единицу выпуска, которую готов заплатить спонсор (см.рис.2)

a/2b Q a/2b Q

Рис.1 Функция «бюджет-выпуск» Рис.2 Функция предельной полезности

Спонсирующие бюро политики обладают правом контроля за его деятельностью, утверждая бюджет и сменяя руководящую команду. Однако спонсор не имеет достаточно стимулов для такого контроля. Дело в том. Что бюро, как правило, выполняют самые разные функции, и контроль за его эффективностью является в первую очередь прерогативой законодателей и избирателей. Поэтому власть спонсора направлена, прежде всего, на захват излишка выпуска бюро. Этот излишек далеко не всегда получает денежное выражение и может реализовываться косвенным образом: путем расширения программ, в которых заинтересованы спонсоры и (или) бюрократы. Такой дележ возможен только в случае, когда бюджет и (или) выпуск бюро больше оптимального.

Теперь о затратах. Предполагается, что бюро покупает ресурсы на конкурентных рынках. Выплачиваемые бюро цены факторов производства отражены функцией, названной Нисканеном «затраты-выпуск» (см. рис.3,4). Предполагается, что C`>0 и C``>0.

Минимальные суммарные выплаты владельцам ресурсов за определенный период обозначим как TC:

TC = cQ + dQ² , 0<Q. (3)

Функция минимальных предельных затрат есть производная от суммарных затрат:

C = c + 2dQ, 0<Q. (4)

TC C

Q Q

Рис.3 Функция «затраты-выпуск» Рис.4 Функция предельных выплат

Предполагается, что функции издержек известны внутри бюро, но не известны окружающим: полная информация об издержках – у сотрудников бюро.

Внутренний мотив деятельности бюрократии – отнюдь не выполнение поставленных задач. Бюрократ движим прежде всего собственными устремлениями, к важнейшим из которых Нисканен относит жалование, служебные привилегии, общественную репутацию (престиж), власть, покровительство вышестоящих чиновников («крыша»), результаты работы учреждения (выпуск бюро), легкость осуществления изменений и управления учреждением. Нисканен исходит из того, что клиентами бюрократии являются парламентарии, которые голосуют за ассигнования и участвуют в работе бюро. бюрократы максимизируют бюджет, полагая, что если этого не делать, то недолго останешься на своем посту. Предполагается, что те, кто обещают больше, чем могут выполнить, получают более скромные бюджеты, а те, кто обещают меньше. Но перевыполняют обещания, «вознаграждаются» большим бюджетом.

Базовая модель является однопериодной. Она строится для простого бюро, оказывающего единственную услугу, которая предоставляется спонсору в обмен на разовый бюджет. Бюро – монопольный поставщик услуги, однако спонсор не использует всю свою потенциальную монопольную власть в качестве ее монопольного покупателя (из-за отсутствия стимулов или возможностей). Предполагается, что бюджет не меньше минимальных общих затрат:

B>TC. (5)

Максимизируя бюджет B, получим Q = a/2b – это и есть максимальный уровень выпуска бюрократии, минимальный уровень достигается при выполнении равенства B` = TC`(Q). Путем соответствующих подстановок (см.1 и 3) получим

Q = a – c / b + d.

Эти два уровня Q равны при a = 2bc /b-d. Тогда равновесный уровень

Q = a-c / b+d, a< 2bc / b-d

Q = a /2b, a > 2bc / b-d (6)

При более низком спросе, представленном функцией предельной ценности V1, равновесный уровень выпуска будет равен Q = a₁ –c / b+d, a₁< 2bc / b-d, и тогда Soa₁gh = Socfh (см. рис. 6). Это означает, что бюджет покрывает минимальные общие затраты и не образует излишка («жира», по терминологии Нисканена). Однако, если выпуск бюро превышает оптимальный уровень, минимально достижимые затраты hf выше, чем hg – предельная ценность для спонсора. Размеры этого выпуска можно найти, приравняв (2) к (4). Тогда оптимальный уровень будет равен Q = a-c / 2(b+d), a> 2bc / b-d. Таким образом, равновесный выпуск оказывается в два раза больше оптимального. Образуется «жир», свидетельствующий о существовании избыточных «производственных мощностей».

Стоимость

a₂ C

V₂ i

a₁ V₁ f

c b

g

o k h j Объем выпуска

a₁ –c/2(b+d) a₁-c/b+d a₂-c/2(b+d) a₂/2b

Рис.6. Равновесный выпуск бюро

Дата добавления: 2014-01-04