Формула Ньютона Лейбница

Теорема (основная теорема интегрального исчисления): Пусть функция f (x) непрерывна на отрезке [ а, b ]. Тогда, если функция F (x) является некоторой первообразной на этом отрезке, то справедлива следующая формула (Ньютона-Лейбница):

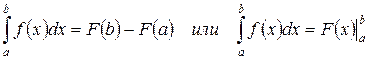
Замена переменной в определённом интеграле (или подстановка в определённом интеграле):

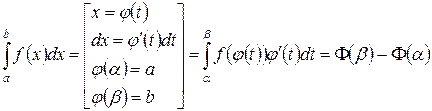
Интегрирование по частям в определённом интеграле:

§79 Геометрические приложения определённого интеграла.

Длина дуги плоской линии:

· в прямоугольных координатах:

Пусть плоская кривая L задана функцией 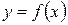непрерывной вместе со своей производной на отрезке [ а, b ], а £ x £ b, тогда длина дуги вычисляется по формуле:

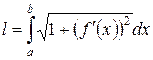
или

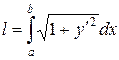
· заданной параметрически:

Пусть кривая L задана параметрическими уравнениями: , a £ t £ b, (где a и b значения параметра t, соответствующие значениям x = а и x = b, то есть а = j (a) и b = j (b)), тогда длина дуги вычисляется по формуле:

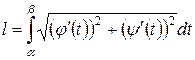
или

· в полярных координатах:

Пусть кривая L задана в полярных координатах функцией непрерывной вместе со своей производной на отрезке [ a,b ], a £ j £ b, тогда длина дуги вычисляется по формуле (a и b значения j):

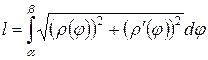
или

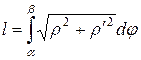
Если кривая L задана в полярных координатах функцией непрерывной вместе со своей производной на отрезке [ a,b ], a £ r £ b, тогда длина дуги вычисляется по формуле(a и b значения r):

или

Площадь криволинейной трапеции:

· в прямоугольных координатах:

Пусть на плоскости Оху дана фигура, ограниченная отрезком [ а, b ] оси Ох, прямыми х = а и х = b и графиком непрерывной функции . Такую фигуру называют криволинейной трапецией.

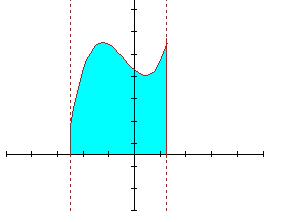Пусть задана неотрицательная функция: , а £ x £ b, тогда площадь криволинейной трапеции (ограниченной сверху 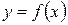, снизу прямой OX, слева прямой х = а, справа прямой х = b) равна:	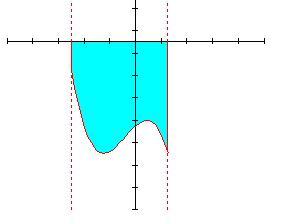Пусть задана неположительная функция: 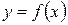, а £ x £ b, тогда площадь криволинейной трапеции (ограниченной сверху OX, снизу прямой 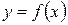, слева прямой х = а, справа прямой х = b):
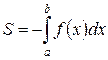
Пусть криволинейная трапеция ограниченной сверх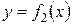у , снизу 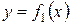, слева прямой х = а, справа прямой х = b) вычисляется по формуле:
	— эта формула справедлива для любых непрерывных функци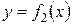й и 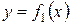, не обязательно положительных, главное, чтобы .
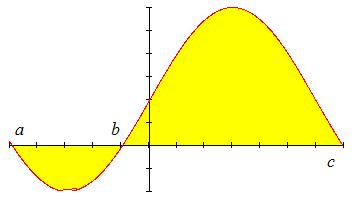
Пусть задана функция, пересекающая ось абсцисс: 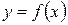, а £ x £ с, тогда площадь криволинейной трапеции (точнее двух криволинейных трапеций, одна находится ниже оси абсцисс, а другая выше) вычисляется по формуле:

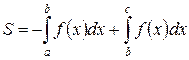
· заданной параметрически:

При вычислении площади криволинейной трапеции в случае, когда верхняя граница задана параметрическими уравнениями: , a £ t £ b, (где a и b значения параметра t, соответствующие значениям x = а и x = b, то есть b = j (b) и а = j (a)), тогда применима формула:

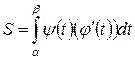
или

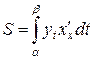
· в полярных координатах:

При вычислении площади криволинейного сектора (ограниченного неотрицательной кривой и двумя полярными радиусами, составляющими с полярной осью углы j ₁= a и j ₂= b применима формула:

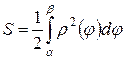
Площадь поверхности вращения:

· в прямоугольных координатах:

вокруг оси Ох: Пусть кривая задана функцией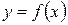, а £ x £ b, которая неотрицательна и непрерывна вместе со своей первой производной на отрезке [ а, b ]. Тогда поверхность, образованная вращением кривой вокруг оси Ох, имеет площадь S, которая может быть вычислена по формуле:

вокруг оси Оу: Пусть кривая задана функцией, c £ у £ d, которая неотрицательна и непрерывна вместе со своей первой производной на отрезке [ c, d ]. Тогда поверхность, образованная вращением кривой вокруг оси Оy, имеет площадь S, которая может быть вычислена по формуле:

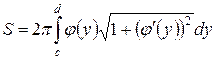
· заданной параметрически:

Если поверхность получается вращением вокруг оси Ох кривой, заданной параметрическими уравнениями , a £ t £ b, (где y (t)³0 a и b значения параметра t, соответствующие значениям x = а и x = b, то есть b = j (b) и а = j (a)), тогда применима формула:

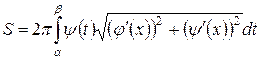
или

· в полярных координатах:

Если кривая задана в полярных координатах уравнением ρ = ρ (φ), a £ j £ b,, где ρ (φ) имеет непрерывную производную на [ a, b ], тогда применима формула:

или

Объём тела вращения:

· в прямоугольных координатах:

вокруг оси Ох: Если тело образовано вращением вокруг оси Ох криволинейной трапеции, заданной непрерывной функцией 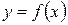, а £ x £ b, объём тела вращения вычисляется по формуле: или

вокруг оси Оу: Если тело образовано вращением вокруг оси Оу криволинейной трапеции, заданной непрерывной функцией , c £ у £ d, объём тела вращения вычисляется по формуле: или

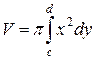
Дата добавления: 2014-01-04