Б. Соединение резистивных элементов

ЛЕКЦИЯ № 7

МЕТОД ЭКВИВАЛЕНТНОГО ПРЕОБРАЗОВАНИЯ СХЕМ

. (1.15)

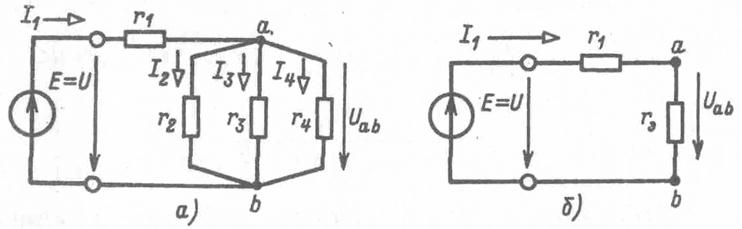
Рис. 1.14

Ток в неразветвленной части

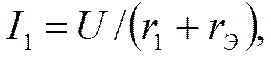
и токи в параллельных ветвях

(1.16)

где

.

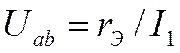по схеме звезды и треуголь­ника

Найдем сопротивление между узлами А и В.

Проводимость между узлами А и В для схемы треугольника на рис. 1.15, а

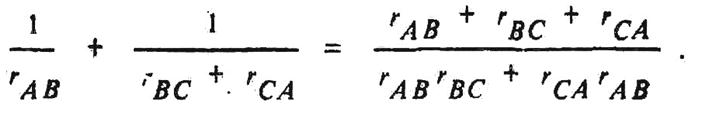
Сопротивление между узлами А и В – величина, обратная проводи­мости между этими узлами, т. е.

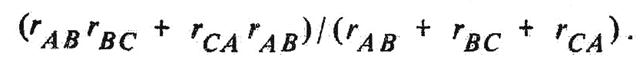
Рис. 1.15

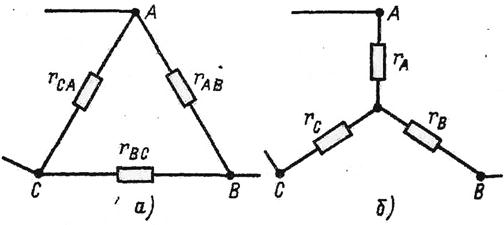
Для схемы звезда на рис. 1.15,б сопротивление между теми же уз­лами А и В равно сумме сопротивлений двух ветвей: .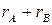

Согласно условию эквивалентности должно выполняться равенство

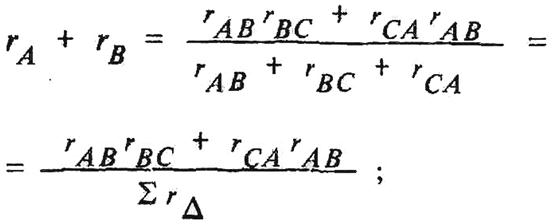(1.17)

здесь 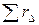–сумма сопротивлений всех ветвей для треугольника.

Структуры треугольника и звезды по отношению к узлам симмет­ричны. Поэтому уравнения равенства сопротивлений между узлами В и С и между узлами С и А можно получить из (1.17) простой цикли­ческой перестановкой индексов:

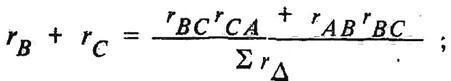(1.18)

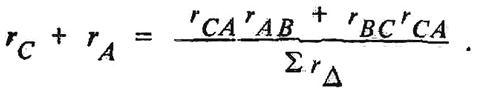(1.19)

Чтобы определить сопротивление r_А звезды, сложим (1.17) и (1.19) и вычтем из этой суммы (1.18); разделив последнее на 2, найдем

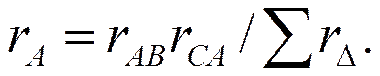(1.20)

Сопротивления других ветвей звезды получим путем циклической перестановки индексов:

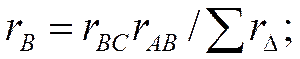(1.21)

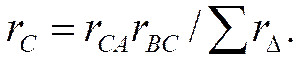(1.22)

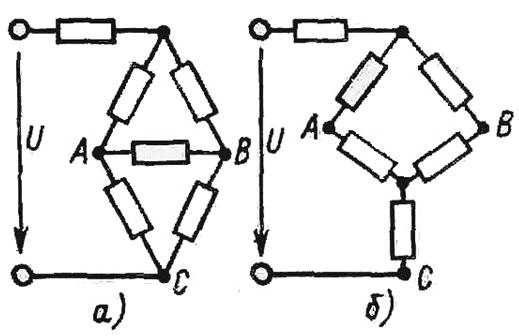
Рис. 1.16

В случае равенства сопротивлений ветвей треугольника (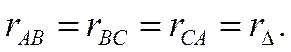) сопротивления ветвей эквивалентной звезды тоже одина­ковы:

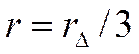. (1.23)

Возможно обратное преобразова­ние звезды из резистивных элемен­тов в эквивалентный треугольник. Для этого перемножим попарно выражения (1.20)–(1.22) и сло­жим полученные произведения:

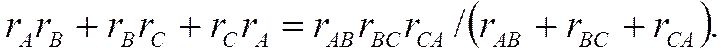
Последнее уравнение разделим на (1.22) и определим сопротивление ветви треугольника:

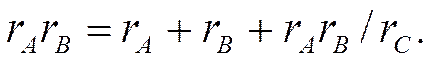(1.24)

Путем циклической перестановки индексов в (1.24) найдем выра­жения для сопротивлений двух других ветвей:

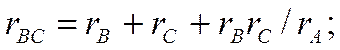(1.25)

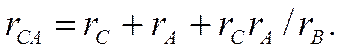(1.26)

Примером упрощения расчетов может служить преобразование мосто­вой схемы соединения резистивных элементов (рис. 1.16, а). После за­мены одного из треугольников эквивалентной звездой всю цепь (рис. 1.16, б) можно рассматривать как смешанное соединение резистивных элементов.

Дата добавления: 2014-01-04