Побудова довірчих границь і інтервалів

Для побудови довірчого інтервалу (чи границі) необхідно знати закон розподілу статистики z=z (x₁,...,x_n), по якій оцінюється невідомий параметр (такою статистикою може бути оцінка z = â (x₁,...,x_n)). Один зі способів побудови полягає в наступному. Припустимо, що деяка випадкова величина j = j(z, a), що залежить від статистики z і невідомого параметра a така, що

1) закон розподілу відомий і не залежить від a;

2) j(z, a) є неперервною та монотонною по .

Виберемо діапазон для - інтервал 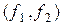так, щоб влучення в нього було практично вірогідно:

P{ f1 £ j(z, a) £ f2 } ³ PД, (3.1)

для чого досить у якості і 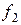взяти квантилі розподілу рівня (1- Р_Д)/2 і (1+ Р_Д)/2 відповідно. Перейдемо в (3.1) до іншого запису випадкової події. Розв’язуючи нерівності щодо параметра a, одержимо (думаючи, що монотонно зростає по ):

P{ g(z, f1) £ a £ g(z, f2) } ³ PД.

Це співвідношення вірне при будь-якім значенні параметра a (оскільки це так для (1)), і тому, відповідно до визначення, випадковий інтервал (g (z, f₁), g (z, f₂)) є довірчим для a з рівнем довіри Р_Д. Якщо спадає по , інтервалом є (g (z, f₂), g (z, f₁)).

Для побудови однобічної границі для a виберемо значення і 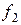так, щоб

P{ j(z, a) ³ f₁ } ³ P_Д, f₁=Q (1 - P_Д)

чи P{ j(z, a) £ f₂ } ³ P_Д, f₂ = Q (P_Д),

де 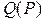- квантиль рівня 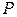. Після розв’язання нерівності під знаком 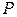одержимо однобічні довірчі границі для a.

Приклад 3.3. Довірчий інтервал з рівнем довіри Р_Д для середнього a нормальної сукупності при відомій дисперсії s ².

Нехай x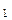,..., x_n - вибірка з нормальної N (a, s) сукупності. Спроможною оцінкою для а є â = â (x,...,x_n) = , розподілена за законом N (a, ).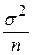

Введемо її нумерацію, утворивши випадкову величину

, (3.2)

яка розподілена нормально N (0, 1) при будь-якім значенні а.

По заданому рівні довіри Р_Д визначимо для j відрізок [- f_p, f_p ] так, щоб

, (3.3)

тобто f_p - квантиль порядку (1+ Р_Д)/2 розподілу N (0,1); помітимо, що j залежить від а, але (3.3) вірно при будь-якім значенні а. Підставимо в (3.3) виразу для j з (3.2) і розв’язуючи нерівність під знаком ймовірності в (3.3) відносно а; одержимо співвідношення

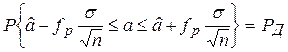, (3.4)

виконується при будь-якім значенні а. Під знаком імовірності дві функції спостережень

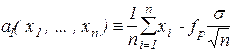, (3.5)

визначають випадковий інтервал

I (x₁,..., x_n) =(a₁ (x₁,..., x_n), a₂ (x₁,..., x_n)), (3.5a)

який у силу (3.4) накриває невідоме значення параметра а з великою імовірністю Р_Д при будь-якому значенні а, і тому, по визначенню довірчого інтервалу, він є довірчим з рівнем довіри Р_Д.

У загальному випадку випадкову величину j у (1) можна побудувати таким чином. Визначимо функцію розподілу F (z / a) статистики z (F, звичайно, залежить від а). Для неперервної z випадкова величина j (z, а) º F(z / a), як неважко бачити, розподілена рівномірно на відрізку [0, 1] при будь-якім значенні а; прийнявши f₁= (1- P_Д)/ 2, f₂ = (1+P_Д)/ 2, будемо мати (3.4) у вигляді

P{f1 £ F (z / a) £ f ₂} = P_Д.

Для дискретної z ситуація аналогічна.

Можна міркувати інакше: при будь-якому фіксованому значенні а визначимо відрізок [ z ₁(a), z ₂(a) ] так, що

P{ z₁ (a) £ z £ z₂ (a) } ³ Р_Д; (3.6)

ясно, що в якості z₁ і z₂ можна взяти квантилі, тобто визначити з умов

F (z _!/ a)=(1- Р_Д)/ 2, F (z ₂/ a)=(1+ Р_Д)/ 2.

Якщо z₁ (a) і z₂ (a) монотонно зростають по а, то, розв’язуючи дві нерівності під знаком Р в (3.6) і беручи до уваги те, що z ₁(a) < z ₂(a), одержимо:

P{ z ₂^-1(z) £ a £ z₁^-1(z) } ³ Р_{Д ,}

є вірним при будь-якому а; ясно, що інтервал (z₂^-1 (z), z₁^-1 (z)), обумовлений двома функціями від z, є довірчим з рівнем довіри Р _Д.

Дата добавления: 2014-01-04