Слабая фокусировка

Орбитальная устойчивость частиц.

Qvo Um / wod {cos[(wo (t2+t1)/2]sin[wo(t2-t1)/2]}.

Время пролета частицей ускоряющего промежутка Dt =d/v_o, тогда

DW_п = qU_msin(f /2)/(f /2) cos (w_ot₁+ f /2) = qU_m n cos (w_ot₁+ f /2),

где f=w_oDt – так называемый угол пролета, n=sin(f/2)/(f/2) ­– коэффициент эффективности взаимодействия частицы с высокочастотным полем ускоряющего промежутка.

Величина n максимальна при f, стремящемся к нулю, что обычно имеет место в ускоряющем промежутке ускорителей. При этом максимальное приращение энергии (f® 0, n ® 1) равно:

DW_п = q U_mcosj,

где j= w_ot₁ – фаза переменного напряжения на ускоряющем промежутке в момент поступления в него частицы.

Тогда уравнение движения частицы в одномерном электрическом поле имеет вид:

m_od²Х/dt² = qE_m cos(w_ot+ f_н),

где f_н – фаза, соответствующая моменту попадания электрона в высокочастотное ускоряющее поле.

После интегрирования этого уравнения при нулевых начальных условиях получим:

X = - qE_m/w_o²m_o cos (w_ot+ f_н) + qE_mt/w_om_o sin f_н.

Из этого уравнения следует, что электрон в высокочастотном электрическом поле совершает колебания с амплитудой qE_m/w_o²m_o и одновременно движется поступательно с постоянной скоростью qE_m/w_om_o. Скорость поступательного движения зависит от фазы, и только те электроны, фаза которых кратна kp (k=0, 1, 2 …) или близка к ней, могут находиться в высокочастотном промежутке продолжительное время.

В реальных ускорителях из-за взаимодействия частиц с молекулами остаточного газа, кулоновского взаимодействия друг с другом, неточности сборки электромагнитов частицы отклоняются от своей траектории. Поэтому в ускорителях необходима фокусировка. Она достигается обычно выбором конфигурации магнитного поля в области движения частиц. Различают слабую (мягкую) и сильную (жесткую) фокусировки.

Смещение частицы от своей орбиты можно в общем случае представить в виде двух независимых смещений: радиального (в плоскости орбиты) и вертикального (аксиального). Поэтому в ускорителях проводится радиальная и аксиальная фокусировки.

Можно показать, что движение частицы оказывается устойчивым в случае, если индукция поля убывает при увеличении радиуса по закону:

В = В_о(r_o /r)ⁿ, 0<n<1.

где В и В_о – индукция магнитного поля при произвольном значении r и при равновесной орбите r_o, n-показатель спада магнитного поля.

Ускорители, в которых выполняется данное условие, называются слабофокусирующими. Поле, описываемое этой зависимостью, создается полюсами магнита, когда расстояние между ними постепенно увеличивается от центра к краям (рис.17).

При этом аксиальная составляющая поля в любой точке имеет постоянное направление и обуславливает силу Лоренца, направленную к оси z, а радиальная составляющая – силу, всегда направленную к плоскости равновесной орбиты, т.е. является фокусирующей.

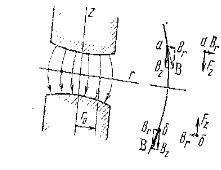
Рис.17. Магнитное поле слабофокусирующего ускорителя.

Движение в аксиальном направлении происходит под действием силы

F_z=qvB_r=md²z/dt², т.е. d²z/dt²= qvB_r/m.

Можно показать, что радиальная составляющая магнитного поля описывается выражением:

B_r=-nzB/r.

Таким образом, фокусирующая сила F_z пропорциональна отклонению z частицы от плоскости равновесной орбиты, т.е. движение электрона под действием вертикальной фокусирующей силы носит колебательный характер и описывается уравнением:

d²z/dt² + nvzqB/(rm)=0

Так как v/r=w, и qB/m=w, где w– круговая частота обращения частицы по орбите, то это уравнение принимает вид:

d²z/dt² + w ²nz = 0.

Рассмотрим радиальную фокусировку частиц. Условие движение частицы по круговой орбите в магнитном поле имеет вид:

mv²/r=qvB=qv В_о(r_o/r)ⁿ

Так как n<1, то при любом изменении радиуса траектории вследствие отклонения частицы от состояния равновесия, результирующая сила стремится вернуть частицу к равновесной орбите. Иными словами, в этих условиях частица, отклонившаяся в радиальном направлении, будет совершать радиальные колебания относительно стационарной орбиты. Уравнение движения имеет вид

d²R/dt² + w² (1-n)R = 0.

где R=r-r_o – радиальное смещение частицы от равновесной орбиты, w–частота обращения частицы по окружности.

Радиальная устойчивость не может быть достигнута при условии n>1: если частица отклонится к центру, то радиус ее орбиты будет непрерывно уменьшаться, а от центра - увеличиваться.

Решения указанных уравнений имеют вид свободных гармонических колебаний (так называемые бетатронные колебания):

Z= A_zsin(n^1/2 w t)= A_zsin(w_zt), R= A_rsin((1-n)^1/2wt)= A_rsin(w_rt),

где A – амплитуды колебаний, а w_z = wn^1/2, w_r =w(1-n)^1/2 – частоты колебаний в направлении z и r.

Конечная энергия частиц, которую можно получить в ускорителе, равна

W=300B_or_o.

Значение В ограничено (обычно 1-2 Тл), и энергию можно увеличить за счет радиуса равновесной орбиты r_o. Однако это приводит к росту амплитуды аксиальных и радиальных колебаний, что вызывает необходимость увеличения размеров ускорительной камеры. Поэтому за счет слабой фокусировки ускорять частицы до высокой энергии неэффективно.

Дата добавления: 2014-01-04