
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 14. Тема 4.1 Электромагнитная задача
|
|
|
|
Тема 4.1 Электромагнитная задача. Постановка проблемы. Алгоритм решения МКЭ
В общем случае процесс непрерывного индукционного нагрева описывается системой уравнений Максвелла для электромагнитного с соответствующими краевыми условиями.
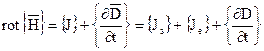 (1)
(1)
 (2)
(2)
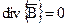 (3)
(3)
 (4)
(4)
Здесь { H}, { B }, { D } – векторы напряженности магнитного поля, магнитной и электрической индукции, 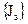 – вектор плотности приложенного тока,
– вектор плотности приложенного тока,  – вектор плотности индуцированного тока,
– вектор плотности индуцированного тока,
Вышеприведенные уравнения описывают связь между различными средами, входящими в систему. Индукционный нагрев на средних частотах характеризуется отсутствием свободных зарядов в системе рассматриваемых сред, поэтому из системы уравнений (1)..(4) можно исключить уравнение (4). Кроме того, обоснованны следующие допущения:
1. Поле принимается квазистационарным. Под этим понимается отсутствие запаздывания электромагнитной волны в воздухе (но не в металле). Это допущение позволяет пренебречь токами смещения по сравнению с токами в проводниках.
2. Не учитываются потери на гистерезис при нагреве ферромагнитных тел в силу их незначительности по сравнению с потерями от вихревых токов.
Принятые допущения позволяют упростить решение рассматриваемой задачи.
Граница раздела магнитных сред описывается системой:
 (7)
(7)
Последнее выражение учитывает скачок вектора 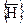 на границе раздела сред.
на границе раздела сред.
При  тангенциальные составляющие напряженности
тангенциальные составляющие напряженности 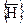 на границе раздела непрерывны
на границе раздела непрерывны
 (8)
(8)
Кроме этого необходимо задать:
- уравнения поверхностей, отделяющих друг от друга среды i и j, fij(x,y,z)=0;
- начальные величины E0(x,y,z), H0(x,y,z) в момент времени t 0 в произвольной точке исследуемого объема  с границей S;
с границей S;
- касательные составляющие вектора 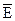 или
или  в произвольной точке поверхности в произвольном временном интервале от t0 до t, или распределения полей
в произвольной точке поверхности в произвольном временном интервале от t0 до t, или распределения полей 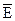 и
и  вне исследуемого объема V;
вне исследуемого объема V;
- функциональные зависимости параметров ε, μ, γ от координат пространства или от напряженности соответствующего поля.
При индукционном нагреве на средних частотах влиянием электрической индукции можно пренебречь. Отсутствие в рассматриваемой системе движущихся постоянных магнитов также исключает появление дополнительных источников внутри проводящих материалов. Тогда связь между напряженностью электрического поля и плотностью токов будет иметь вид
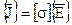 , (12)
, (12)
Решение задачи электромагнитного поля достигается использованием векторного магнитного потенциала { A } и скалярного электрического потенциала V, которые выражаются следующим образом:
 (14)
(14)
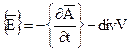 (15)
(15)
Чтобы функция 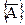 была определена, нужно определить значение ее дивергенции. Для этого добавляется условие, которое называется калибровкой Кулона
была определена, нужно определить значение ее дивергенции. Для этого добавляется условие, которое называется калибровкой Кулона
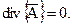 (16)
(16)
В результате получим следующую систему уравнений
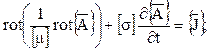 (17)
(17)
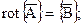 (18)
(18)
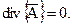 (19)
(19)
Используя соотношение
 (20)
(20)
при μ =const из (17) получим уравнение
 (21)
(21)
Уравнение Пуассона (21) дополняется граничными условиями Дирихле и Неймана на различных участках границы:

 на S1 (22)
на S1 (22)
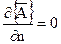 на S2 (23)
на S2 (23)
Такое упрощение условий задачи объясняется тем, что дальнейший переход к конечно-элементной формулировке намного облегчается для линейной задачи. Реальные нелинейные задачи решаются на базе линейных моделей с помощью итерационных алгоритмов расчета.
Решение краевой задачи расчета магнитного поля в изотропной среде (21)..(23) эквивалентно минимизации энергетического функционала:
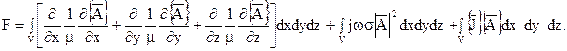 (24)
(24)
Сущность метода, основанного на МКЭ, заключается в исследовании глобальной функции процесса, в данном случае векторного потенциала  , в дискретных частях анализируемой области V, которая должна быть предварительно разбита на конечные смежные подобласти (конечные элементы), что позволяет свести задачу с бесконечным числом степеней свободы к задаче, содержащей конечное число параметров. При этом внутри подобластей искомая функция интерполируется степенными полиномами, сшивается на границах контакта элементов, и при условии малости геометрических размеров последних (число элементов стремится к бесконечности), оказывается решением уравнений в частных производных типа (21)..(23). В качестве интерполирующих полиномов конечных элементов треугольного вида использованы линейные функции формы вида:
, в дискретных частях анализируемой области V, которая должна быть предварительно разбита на конечные смежные подобласти (конечные элементы), что позволяет свести задачу с бесконечным числом степеней свободы к задаче, содержащей конечное число параметров. При этом внутри подобластей искомая функция интерполируется степенными полиномами, сшивается на границах контакта элементов, и при условии малости геометрических размеров последних (число элементов стремится к бесконечности), оказывается решением уравнений в частных производных типа (21)..(23). В качестве интерполирующих полиномов конечных элементов треугольного вида использованы линейные функции формы вида:
 (25)
(25)
Треугольные элементы позволяют наиболее просто аппроксимировать сложные геометрические границы тел. В настоящее время разработаны другие виды конечных элементов, например четырехугольные с криволинейными сторонами, что обеспечивает при сравнительно небольшом числе элементов гладкую аппроксимацию контуров области. Такая же ситуация имеет место и для объемных областей. Дальнейшие рассуждения проведем для более простой плоской задачи.
В результате векторный потенциал внутри m – го элемента треугольника определяется значениями потенциала в вершинах треугольника, то есть является линейной функцией координат x и y.
 (26)
(26)
где: 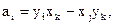

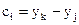 - постоянные коэффициенты функций формы Ni, вычисляемые в зависимости от пространственных координат узлов элемента m;
- постоянные коэффициенты функций формы Ni, вычисляемые в зависимости от пространственных координат узлов элемента m; 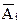 - комплексные амплитуды вектора в узлах конечного элемента.
- комплексные амплитуды вектора в узлах конечного элемента.
В дискретной модели функционал (24) определяется суммой вкладов всех КЭ, входящих в ансамбль
 , (27)
, (27)
а условие его минимума приобретает вид
 (28)
(28)
где Ne – полное число всех элементов.
Дифференцирование по 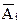 дает результат, отличный от нуля только в том случае, если i является одной из вершин текущего треугольника. Следовательно, для каждого элемента можно построить свой блок элементных матриц, отражающих вклад данного КЭ в энергетический функционал (24).
дает результат, отличный от нуля только в том случае, если i является одной из вершин текущего треугольника. Следовательно, для каждого элемента можно построить свой блок элементных матриц, отражающих вклад данного КЭ в энергетический функционал (24).
Матрица жесткости определяется следующим выражением:
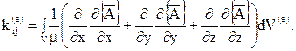 (29)
(29)
Матрица вихревых токов рассчитывается следующим образом
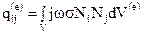 . (30)
. (30)
Матрица внешних источников тока вычисляется согласно выражению
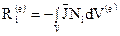 (31)
(31)
В последнем выражении плотность внешних источников тока внутри элемента принимается постоянной.
Согласно выражению (28) элементные матрицы (29) должны объединяться в глобальные матрицы, характеризующие поведение дискретной системы в целом.
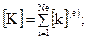
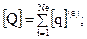
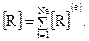 (32)
(32)
В результате ансамблирования получаем систему алгебраических уравнений:
 (33)
(33)
Решение данной задачи осуществляется итерационным методом. Краевые условия вида Дирихле учитываются путем принудительного исключения столбцов и строк глобальных матриц (32), относящихся к узлам дискретной системы, лежащих на удаленных границах S области V. Условия симметрии удовлетворяются при ансамблировании элементов автоматически. Распределенные параметры магнитного поля вычисляются по выражению (18):
 ; (34)
; (34)
 (35)
(35)
 . (36)
. (36)
Напряженность электрического поля
 . (37)
. (37)
Мощность внутренних источников тепла, характеризующих нагрев проводящих тел индукционной системы, вычисляется для каждого элемента по закону Джоуля-Ленца
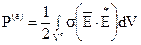 , (38)
, (38)
где 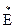 - величина, сопряженная к
- величина, сопряженная к 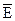 .
.
Кроме этого, рассчитываются также электродинамические усилия, действующие на проводящие тела индукционной системы.
Магнитные силы в токопроводящем проводнике определяются численным интегрированием
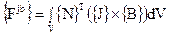 (39)
(39)
Тензор напряжений Максвелла используется для определения сил в ферромагнитных областях. Эта сила рассчитывается на внешней поверхности элемента, которая имеет ненулевую грань нагружения. Для двумерного случая имеет место выражение
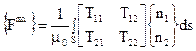 (40)
(40)
 (41)
(41)
 (42)
(42)
 (43)
(43)
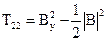 (44)
(44)
Для учета нелинейной зависимости 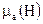 в ферромагнитных областях используется итерационный алгоритм многократного решения результирующей системы уравнений (33). В начальной стадии расчета задается значение μ =const по всей области ферромагнитных макроэлементов, затем вычисляются распределенные параметры поля, что позволяет на следующей стадии расчета корректировать μ внутри каждого конечного элемента в зависимости от значения напряженности магнитного поля в данной области. Итерации повторяются до полной сходимости процесса. Определение магнитной проницаемости производится с помощью введения в программу расчета полинома, аппроксимирующего кривую намагничивания.
в ферромагнитных областях используется итерационный алгоритм многократного решения результирующей системы уравнений (33). В начальной стадии расчета задается значение μ =const по всей области ферромагнитных макроэлементов, затем вычисляются распределенные параметры поля, что позволяет на следующей стадии расчета корректировать μ внутри каждого конечного элемента в зависимости от значения напряженности магнитного поля в данной области. Итерации повторяются до полной сходимости процесса. Определение магнитной проницаемости производится с помощью введения в программу расчета полинома, аппроксимирующего кривую намагничивания.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 329; Нарушение авторских прав?; Мы поможем в написании вашей работы!