Свойства основных кривых распределения. Графический метод изучения рядов распределения

Кривая линия, которая отражает закономерность изменения частот (частностей) в чистом, исключающем влияние случайных факторов, виде называют кривой распределения. Кривая распределения, в отличие от полигона и гистограммы, отражает основной характер, закон данного распределения. В идеальном случае зависимость частот (частностей, плотности распределения) от величины вариантов может быть предоставлена в виде некоторой кривой распределения определенного вида (типа).
Построение кривой распределения в сочетании с анализом сущности явления позволяют построить научную гипотезу о вероятном типе теоретической кривой распределения. Под теоретической кривой распределения в статистике понимается предполагаемое графическое изображение в виде непрерывной линии изменения частот в вариационном ряду функционально связанного с изменением (величины признака) варианты.

В действительности встречаются самые различные типы распределения. В связи с этим различаются прежде всего одновершинные (одномодальные) и многовершинные (многомодальные) кривые распределения. К одновершинным относятся те, в которых один вариант имеет наибольшую частоту (наибольшую плотность распределения), частоты же вариантов меньших и больших, чем это значение, убывают по мере удаления от него. Если при этом частоты убывают одинаково и справа и слева от наибольшего центрального значения, то такие распределения называются симметричными. В них частоты вариантов, равностоящих от центрального, равны между собой.
Если частоты убывают слева и справа от центра распределения с разной скоростью, то такие распределения называются ассиметричными, выделяя при этом распределения, растянутые влево или вправо.

Степень асимметрии может быть различной от совершенно незначительной до крайней, при которой наибольшая частота относится к одному из крайних значений вариантов – самому наименьшему или наибольшему. Идеальное симметричное распределение крайне редко встречаются на практике. Основная масса распределений, с которыми приходиться иметь дело экономисту – это асимметричные распределения с разной степенью асимметрий. Многовершинные распределения – это такие распределения, в которых несколько максимумов частоты (центральных значений признака). В экономико – статистических исследованиях многовершинность распределения является часто следствием того, что совокупность состоит из неоднородных с точки зрения изучаемого признака единиц.
Например, при проверке качества и свойств продукции, полученной на двух разных станках, почти всегда получаются кривые распределения с двумя вершинами. Убедившись в многовершинности распределения, исследователь должен тщательно проверить, можно ли считать однородными единицы, составляющие совокупности или следует для объективности выводов разбить совокупность на две или более однородные группы.

Эксцесс – характеристика островершинности и крутизны распределения. Количественная оценка степени ассиметрии и эксцессы рассматривается в дисциплине «Математическая статистика».

Известно достаточно много форм кривых распределения, по которым может выравниваться вариационный ряд, но в практике статистических исследований наиболее часто используются такие формы, как нормальное распределение и распределение Пуассона.

Нормальное распределение зависит от двух параметров: средней арифметической 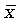и среднего квадратического отклонения . Его кривая выражается уравнением (9.3):

(9.3)

где у – ордината кривой нормального распределения; 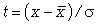- стандартизованные отклонения; е и π – математические постоянные; x – варианты вариационного ряда; 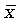- их средняя величина; - cреднее квадратическое отклонение.

Если нужно получить теоретические частоты f' при выравнивании вариационного ряда по кривой нормального распределения, то можно воспользоваться формулой 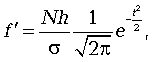(9.4):

(9.4)

где 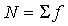- сумма всех эмпирических частот вариационного ряда; h - величина интервала в группах; - cреднее квадратическое отклонение; 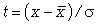- нормированное отклонение вариантов от средней арифметической; все остальные величины легко вычисляются по специальным таблицам.

Если вариационный ряд представляет собой распределение по дискретному признаку, где при увеличении значений признака х частоты начинают резко уменьшаться, а средняя арифметическая, в свою очередь, равна или близка по значению к дисперсии (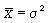), то такой ряд выравнивается по кривой Пуассона.

Кривую Пуассона можно выразить отношением 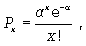(9.5):

(9.5)

где P_x - вероятность наступления отдельных значений х; 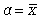- средняя арифметическая ряда.

При выравнивании эмпирических данных теоретические частоты можно определить по формуле 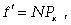(9.6):

(9.6)

где f' – теоретические частоты; N – общее число единиц ряда.

Сравнивая полученные величины теоретических частот f' c эмпирическими (фактическими) частотами f, убеждаемся, что их расхождения могут быть весьма невелики. Объективная характеристика соответствия теоретических и эмпирических частот может быть получена при помощи специальных статистических показателей, которые называют критериями согласия.

Для оценки близости эмпирических и теоретических частот применяются критерий согласия Пирсона, критерий согласия Романовского, критерий согласия Колмогорова.

Наиболее распространенным является критерий согласия Пирсона 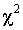, который можно представить как сумму отношений квадратов расхождений между f' и f к теоретическим частотам (9.7):

(9.7)

Вычисленное значение критерия 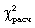необходимо сравнить с табличным (критическим) значением 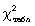. Табличное значение определяется по специальной таблице, оно зависит от принятой вероятности Р и числа степеней свободы k (при этом k = m - 3, где m - число групп в ряду распределения для нормального распределения). При расчете критерия согласия Пирсона должно соблюдаться следующее условие: достаточно большим должно быть число наблюдений (n 50), при этом если в некоторых интервалах теоретические частоты < 5, то интервалы объединяют для условия > 5. Если , то расхождения между эмпирическими и теоретическими частотами распределения могут быть случайными и предположение о близости эмпирического распределения к нормальному не может быть отвергнуто.

В том случае, если отсутствуют таблицы для оценки случайности расхождения теоретических и эмпирических частот, можно использовать критерий согласия Романовского К_Ром, который, используя величину 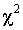, предложил оценивать близость эмпирического распределения кривой нормального распределения при помощи отношения (9.8):

(9.8)

где m - число групп; k = (m - 3) - число степеней свободы при исчислении частот нормального распределения.

Если вышеуказанное отношение < 3, то расхождения эмпирических и теоретических частот можно считать случайными, а эмпирическое распределение - соответствующим нормальному. Если отношение > 3, то расхождения могут быть достаточно существенными и гипотезу о нормальном распределении следует отвергнуть.

Критерий согласия Колмогорова 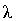используется при определении максимального расхождения между частотами эмпирического и теоретического распределения и вычисляется по формуле (9.9):

(9.9)

где D - максимальное значение разности между накопленными эмпирическими и теоретическими частотами; 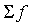- сумма эмпирических частот.

По таблицам значений вероятностей 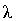-критерия можно найти величину 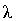, соответствующую вероятности Р. Если величина вероятности Р значительна по отношению к найденной величине 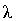, то можно предположить, что расхождения между теоретическим и эмпирическим распределениями несущественны. Необходимым условием при использовании критерия согласия Колмогорова является достаточно большое число наблюдений (не меньше ста).

Для конкретного графического изображения рядов распределения в статистике используются следующие виды графиков:

1) полигон распределения - дискретные ряды изображаются с помощью линий, перпендикулярных соответствующим значениям вариант; высота линий определяется частотой варианты;

2) гистограмма распределения – интервальный вариационный ряд изображается в виде прямоугольников, построенных на оси х; ширина прямоугольников соответствует интервалу, а высота пропорциональна соответствующей частоте (если в таком графике середины верхних сторон прямоугольников соединить прямыми, получится полигон распределения);

3) кумулята – накопленные частоты наносятся на график виде перпендикуляров к оси х в точках, отмечающих полусуммы интервалов; вершины перпендикуляров соединяются прямыми, при этом образуется ломаная линия, которая возрастает от нуля до высоты, равной общей сумме частот;

4) кривые концентрации - поле графика стоится виде квадрата, нижняя сторона которого (ось x) будет обозначать накопленные итоги распределения объектов, а левая сторона (ось у) – накопленные итоги их признаков; если бы процесса концентрации не было, кривые распределения признаков совпали бы с линией равномерного распределения.

Дата добавления: 2014-01-04