Понятие и виды статистических рядов

Тема 9. Ряды распределения

Статистические ряды распределения – это первичная характеристика массовой статистической совокупности, упорядоченное разложение единиц изучаемой совокупности на группы по группировочному признаку. Любой статистический ряд распределения состоит из двух элементов:

1) отдельных значений варьирующего признака (вариантов);

2) величин, которые показывают, сколько раз повторяется данная варианта (частот ).

Примечание. Частоты, выраженные в долях единицы или в процентах к итогу, называются частостями; это численность ряда распределения выражается суммой частот.

Если за основу группировки взят качественный признак, то такой ряд распределения называют атрибутивным (распределение по видам труда, по полу, по профессии, по религиозному признаку, национальной принадлежности и т.д.). Если ряд распределения построен по количественному признаку, то такой ряд называют вариационным. Построить вариационный ряд - значит упорядочить количественное распределение единиц совокупности по значениям признака, а затем подсчитать числа единиц совокупности с этими значениями (построить групповую таблицу).

Выделяют три формы вариационного ряда:

1) ранжированный ряд - это распределение отдельных единиц совокупности в порядке возрастания или убывания исследуемого признака; ранжирование позволяет легко разделить количественные данные по группам, сразу обнаружить наименьшее и наибольшее значения признака, выделить значения, которые чаще всего повторяются; другие формы вариационного ряда - групповые таблицы, составленные по характеру вариации значений изучаемого признака;

2) дискретный ряд - это такой вариационный ряд, в основу построения которого положены признаки с прерывным изменением, между которыми нет промежуточных значений (дискретные признаки - тарифный разряд, количество детей в семье, число работников на предприятии и т.д.); эти признаки могут принимать только конечное число определенных значений;

Дискретный ряд представляет собой групповую таблицу, которая состоит из двух граф: в первой графе указывается конкретное значение признака, а во второй - число единиц совокупности с определенным значением признака;

3) если признак имеет непрерывное изменение (размер дохода, стаж работы, стоимость основных фондов предприятия и т.д., которые в определенных границах могут принимать любые значения), то для этого признака нужно строить интервальный ряд (с равными или неравными интервалами).

Групповая таблица здесь также имеет две графы. В первой указывается значение признака в интервале «от - до» (варианты), во второй - число единиц, входящих в интервал (частота). Очень часто таблица дополняется графой, в которой подсчитываются накопленные частоты S, которые показывают, какое количество единиц совокупности имеет значение признака не большее, чем данное значение. Частоты ряда f могут заменяться частностями w, выраженными в относительных числах (долях или процентах). Они представляют собой отношения частот каждого интервала к их общей сумме (9.1):

(9.1)

При построении вариационного ряда с интервальными значениями, прежде всего, необходимо установить величину интервала i, которая определяется как отношение размаха вариации R к числу групп n (9.2):

i = 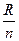, (9.2)

где R = x_max - x_min; n = 1 + 3,322 lgN(формула Стерджесса); N - общее число единиц совокупности.

Интервальные вариационные ряды могут быть построены и для признаков с дискретной вариацией. Нередко в статистическом исследовании указывать отдельное значение дискретного признака нецелесообразно, т.к. это, как правило, затрудняет рассмотрение вариации признака. Поэтому возможные дискретные значения признака распределяются по группам и подсчитываются соответствующие им частоты (частности). При построении интервального ряда по дискретному признаку границы смежных интервалов не повторяют друг друга: следующий интервал начинается со следующего по порядку (после верхнего значения предыдущего интервала) дискретного значения признака.

При сравнении частот ряда с неравными интервалами для характеристики их наполненности рассчитывают плотность распределения. Средняя плотность в интервале – это частное от деления частоты и частности на величину интервала. В первом случае плотность абсолютная, во втором – относительная. Средняя плотность показывает, сколько единиц или их процентов приходится на единицу измерения варианты. Частота, частность, плотность и накопленная частота – это различные функции от величины варианты.

В процессе анализа статистических данных, представленных рядами распределения, кроме знания о характере распределения (или структуре совокупности) могут вычисляться различные статистические показатели (числовые характеристики), которые в обобщенном виде отражают особенности распределения изучаемых признаков. Эти характеристики (показатели) могут быть разделены на 3 основные группы

1 ) характеристики центра распределения (средняя, мода, медиана);

2) характеристики степени вариации (вариационный размах, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации);

3) характеристики формы (типа) распределения (показатели эксцесса и асимметрии, ранговые характеристики, кривые распределения).

Наиболее надежный путь выявления закономерности распределения состоит в следующем:
1) увеличить количество наблюдаемых случаев (в соответствии с законом больших чисел, в таких рядах случайные отклонения от общей закономерности у индивидуальных значений будут взаимно погашаться);

2) первоначально совокупность разбить на максимальное возможное число групп, затем, постепенно сокращая число групп, оптимизировать группировку с точки зрения выявления закономерности распределения.

При реализации такого подхода закономерность, характерная для данного распределения будет выступать все более и более ясно, а ломаная линия, изображающая полигон, будет приближаться к некоторой плавной линии и в пределе должна превратиться в кривую линию.

Дата добавления: 2014-01-04