
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Производная по направлению
|
|
|
|
Дана функция U=f(x,y,z), дифференцируемая в точке M(x,y,z). Дадим x,y,z приращение 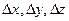 .
.
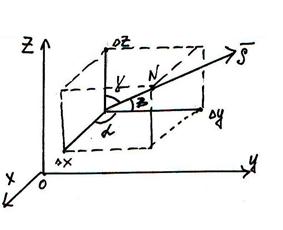 Соединим M и N. Проведем диагональ и обозначим вектор
Соединим M и N. Проведем диагональ и обозначим вектор  Известны направляющие косинусы
Известны направляющие косинусы 
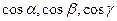
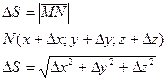
Т.к. функция u=f(x,y,z) дифференцируема в точке M(x,y,z), то её полное
приращение представимо в виде:
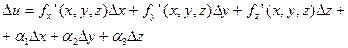
где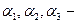 бесконечно малые при
бесконечно малые при 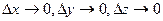 т.е.
т.е. 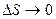
Разделим обе части равенства на 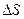 :
:
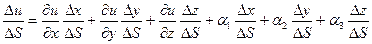
Но:
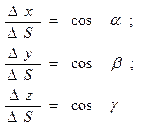
Тогда: 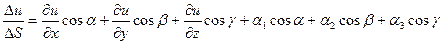
Перейдём к пределу при 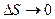 :
:

Опр. Если существует предел 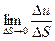 , то он называется производной от
, то он называется производной от
функции u=f(x,y,z) по направлению S и обозначается: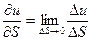
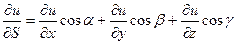
Пример. Найти производную функции u=xy2+z3-xyz в точке М(1;1;2) в направлении, образующимся осями координат (углы:60°,45°,60°). 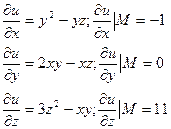
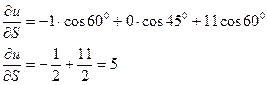
Градиент функции
Дана функция u=f(x,y,z)
Опр. Вектор, координатами которого являются частные производные от функции u=f(x,y,z), называется градиентом функции и обозначается:
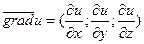
Пример. Найти точки, в которых модуль градиента функции 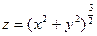 равен 2.
равен 2.
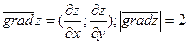 {по условию}
{по условию}
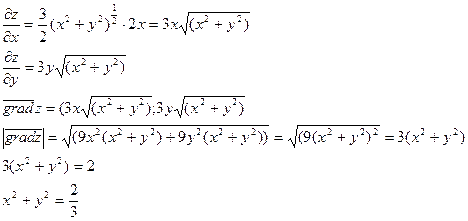
Во всех точках окружности с радиусом  и с центром в начале координат
и с центром в начале координат 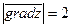
Связь производной по направлению с градиентом
Известно, что: 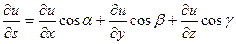 . Введём орт
. Введём орт

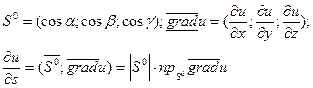 {по свойству скалярного произведения}
{по свойству скалярного произведения}
Ho 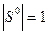 ,значит
,значит 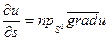
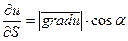

Если 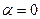 , то
, то 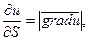 при этом производная по направлению градиента функции достигает наибольшего значения.
при этом производная по направлению градиента функции достигает наибольшего значения.
Если 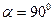 , то
, то 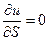 . В направлении
. В направлении 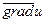 перпендикулярен
перпендикулярен
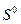 .
.
Экстремум функции двух переменных
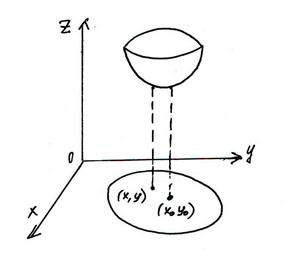 Дана функция z =f(x,y).
Дана функция z =f(x,y).
Точка (x0;y0) называется точкой минимума функции z=f(x,y), если в любой ее окрестности выполняется неравенство: f(x0;y0)<f(x;y)
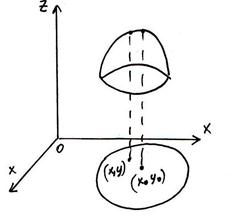 Точка (x0;y0)называется точкой максимума функции z=f(x,y), если в любой ее окрестности выполняется неравенство: f(x0;y0)>f(x,y)
Точка (x0;y0)называется точкой максимума функции z=f(x,y), если в любой ее окрестности выполняется неравенство: f(x0;y0)>f(x,y)
Необходимое условие экстремума функции двух переменных
Если в точке (х0,у0) функция достигает максимума или минимума (если (х0,у0) -
точка экстремума), то в этой точке её частные производные обращаются в нуль или не существуют, т.е. 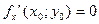 ,
, 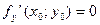 или не существует.
или не существует.
Доказательство: Дано: (х0,у0) - точка экстремума, z=f(x,y).
Дадим у определённое значение у0. Тогда z=f(x,y0) будет функцией одной переменной х и согласно неоходимому условию экстремума функции одной переменной, производная от этой функции равна нулю или не существует т.е. 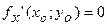 или не существует. Аналогично, положим, что х=х0, тогда z=f(x0,у) - функция одной переменной у и согласно необходимому условию экстремума функции одной переменной
или не существует. Аналогично, положим, что х=х0, тогда z=f(x0,у) - функция одной переменной у и согласно необходимому условию экстремума функции одной переменной 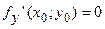 или не существует.
или не существует.
Теорема.Достаточное условие экстремума функции двух переменных
Пусть z=f(x,y) в критической точке (х0,у0) непрерывна и имеет частные
производные включительно до второго порядка, и пусть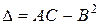 , где
, где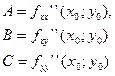 Тогда
Тогда
1. если 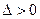 и А<0,то (х0,у0) - точка максимума
и А<0,то (х0,у0) - точка максимума
2. если 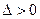 и А>0,то (х0,у0) - точка минимума
и А>0,то (х0,у0) - точка минимума
3. если 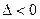 , то экстремума нет.
, то экстремума нет.
4. если 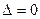 ответа нет, т.е. требуются дополнительные исследования.
ответа нет, т.е. требуются дополнительные исследования.
Пример. Исследовать на экстремум функцию z=x2+3xy-18x-12y.
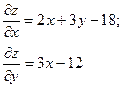
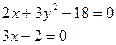
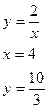 M (4;
M (4;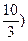
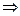
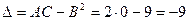
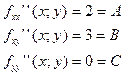 - экстремума нет.
- экстремума нет.
Наибольшее наименьшее значения функции в области
Пусть функция непрерывна в замкнутой области. Тогда по свойству функций, непрерывных в замкнутой области, она достигает в этой области своего наименьшего m и наибольшего М значений. Чтобы найти эти значения, нужно:
1.найти критические точки функции и вычислить значение функции в этих
точках;
2.найти наибольшее и наименьшее значения функции на границах;
3.среди найденных значений функции выбрать наибольшее и наименьшее.
Пример. Найти наибольшее и наименьшее значения функции z=x2+y2 -ху+х+y в области, заданной неравенством: 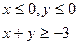
1.Находим критические точки: 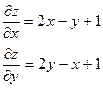
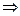 +
+ 
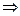
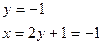
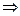 (-1,1)
(-1,1) 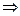 z(-l,-l)=-l.
z(-l,-l)=-l.
2.Исследуем на границе:
а)АО: x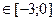 . Уравнение границы: у=0. Линия
. Уравнение границы: у=0. Линия
пересечения у=0 с поверхностью z=x2+у2-ху+х+у имеет вид: z=x2+х (подстановка в уравнение y=0). Задача сводится к отысканию наибольшего, наименьшего значения функции z от -3 до 0.
z (-3)=6;
z (0)=0;
z'=2x+1; 2x+1=0; 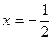
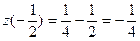
б) OB: x=0; y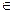 [-3;0]
[-3;0]
Линия пересечения: z=y 2 +у.
z (-3)=0;
z (0)=6; 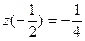
в)АВ: уравнение: х+у=-3; у=-х-3
Линия пересечения: z=x2+(-x-3)2-х(-х-3)+х-х-3; z=3х2+9х+6; х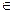 [-3;0].
[-3;0].
z(0)=6; z'=6x+9; 6х+9=0; x=-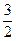
z(-3)=6; 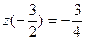
3. Среди найденых значений z выбираем наибольшее и наименьшее: m=-1, М=6.
Условный экстремум
Требуется найти экстремум функции z=f(x,y), при условии, что х и у связаны соотношением: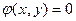 . Такой экстремум называется условным.
. Такой экстремум называется условным.
Равенство 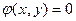 задаёт y как функцию от х неявно. Если бы удалось выразить y через х и подставить в функцию z = f(x,y), то z была бы функцией от одной переменной х. Поэтому в точках экстремума
задаёт y как функцию от х неявно. Если бы удалось выразить y через х и подставить в функцию z = f(x,y), то z была бы функцией от одной переменной х. Поэтому в точках экстремума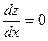 .
.
Найдём (по правилу дифференцирования сложной функции):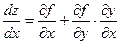 .T.к.
.T.к.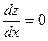 , тo
, тo 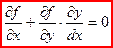 (l).
(l).
Продифференцируем функцию 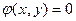 по правилу дифференцирования сложной функции:
по правилу дифференцирования сложной функции: 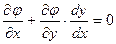 (2).
(2).
Равенство (2) умножим на некоторое число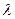 , сложим с равенством (1). Получим:
, сложим с равенством (1). Получим: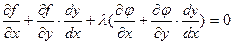 .
.
Раскроем скобки: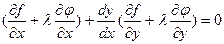 .
.
Подберём 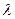 таким образом, чтобы выражение
таким образом, чтобы выражение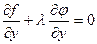 .
.
Тогда 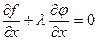 . Добавим уравнение
. Добавим уравнение 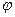 (х,y)=0 и получим систему, которая позволяет найти х, у,
(х,y)=0 и получим систему, которая позволяет найти х, у,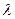 , в которых необходимым условием условного экстремума являются:
, в которых необходимым условием условного экстремума являются: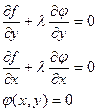 .
.
Для облегчения написания этих условий вводится функция Лагранжа: .
.
Найдём: 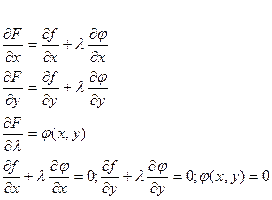
Достаточное условие
Составляется дифференциал: d 2 F=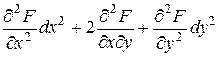 .
.
Если 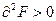 , то (x0,y0,
, то (x0,y0,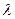 0) - точка условного максимума,
0) - точка условного максимума,
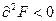 , то
, то  - точка условного минимума.
- точка условного минимума.
Или в следующем виде:
составляется другой вид достаточного условия.

Если 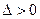 , то точка
, то точка  - точка условного максимума,
- точка условного максимума, 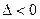 , то точка
, то точка  - точка условного
- точка условного
минимума.
Пример. Найти экстремум функции: z=6-4x-3y при условии, что х2+у2=1 (т.к. лежат на окружности)
 x2+y2-l=0;f(x,y)=z=6-4x-3y;F(x,y,
x2+y2-l=0;f(x,y)=z=6-4x-3y;F(x,y, 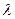 )=6-4х-3у+
)=6-4х-3у+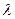 (х2+у 2 -1);
(х2+у 2 -1);

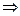
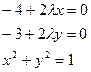
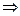
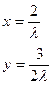
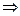
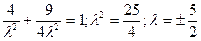
1)
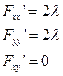
2)
Найдём: 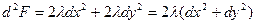
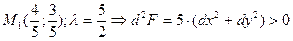 - точка условного максимума;
- точка условного максимума;
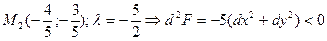 - точка условного минимума.
- точка условного минимума.
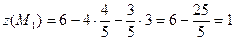
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 665; Нарушение авторских прав?; Мы поможем в написании вашей работы!