Замечание

M

Опр.4 Множество точек называется связным, если любые две точки могут быть соединены непрерывной линией целиком состоящей из точек этого множества.

Примеры связных множеств:

Примеры несвязных множеств:

Множество C – несвязное

A B

Опр.5 Точка М называется внутренней точкой некоторого множества, если любая окрестность этой точки состоит из точек этого множества.

Опр.6 Множество, все точки которого внутренние, называется открытым множеством.

Опр.7 Связанное открытое множество называется областью.

Опр.8 Точка М называется граничной точкой области, если в любой её окрест­ности содержатся как точки, принадлежащие этой области, так и не принадлежащие ей.

Пример. y

Пусть область задаётся: x=-2 4 x=2

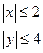
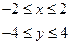x

-2 0 2

т. M - граничная M

-4

Опр.9 Совокупность граничных точек называется границей области.

Опр.10 Область с присоединённой к ней границей называется замкнутой областью.

Геометрическая интерпретация функции двух переменных.

Опр. Графиком функции двух переменных называется геометрическое место то­чек Р (х,у, f(х,у)).

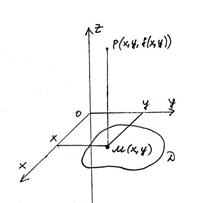
График представляет собой некоторую поверхность.

Пример.

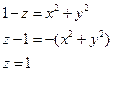
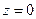
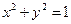- окружность

x = 0 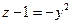- парабола, ветви которой направлены вверх в плоскости XOZ

y = 0 - парабола в плоскости YOZ

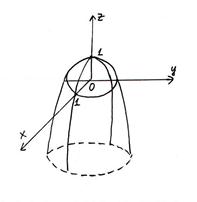
Рассечем поверхность плоскостями z = C – плоскости, параллельные XOY.

Эти плоскости пересекают поверхность некоторыми линиями.

Уравнения этих линий:

f (x, y) = C

Спроектируем эти линии на плоскость XOY

Эти линии называются линиями уровня, то есть это проекции на плоскость XOY линий пересечения поверхности с плоскостями, параллельными плоскостям XOY.

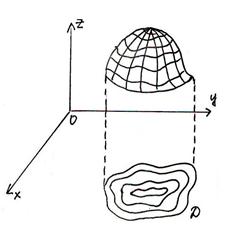
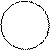
Пример.

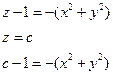
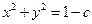- окружности с центром в начале координат и радиусом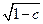

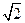
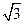2

с = 1

Функции трёх переменных.

Опр. Переменная U называется функцией от трёх переменных x,y,z если каждой тройке действительных чисел (x,y,z) из некоторой области по некоторому правилу или закону ставится в соответствие одно или несколько значений переменной U.

Обозначается: U = f(x,y,z), где x,y,z- независимые переменные.

Пример.

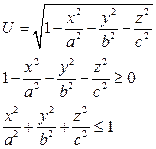
Область определения - внутренность эллипсоида, замкнутая.

Функции п переменных.

Опр. Переменная W называется функцией от n-переменных x,y,z...t, если каждой системе из n чисел (x,y,z…t) по некоторому правилу или закону ставится в соот­ветствие одно или несколько значений переменной W.

Обозначается: W = f(x,y,z...t)

Замечание. Если систему из n чисел обозначить как точку M (x,y,z…t) в n-мерном пространстве, то функцию можно обозначить: W = f(M).

Предел функции двух переменных. Непрерывность.

Дана функция z = f(x,y) в некоторой области D.

Опр.1 Число А называется пределом функции z = f(x,y) при стремлении точки М(х,у) к точке М₀(x₀,у₀), если для любого ε>0 найдётся такое δ >0, такое, что для всех М(х,у), удовлетворяющих неравенству 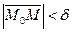выполняется неравентсво .

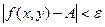Обозначается: limf(x, y) = A; lim f(x, y) = A

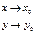
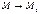
Неравенство 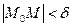означает, что

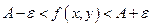
Иначе говоря, для любой 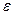-окрестности точки А, сколь угодно малой напе­рёд заданной, найдётся такая ¶ -окрестность точки М, что для всех точек из этой окрестности значение функции не выйдет за пределы плоскостей z = A+ ε и z = A- ε.

Замечание. Все теоремы, изложенные для пределов функции одной переменной, cправедливы и для функции двух переменных.

Пример.

1. lim(x²+y²) = 4+9 = 13;

2. 1im 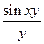= (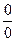) = lim 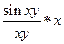= lim x = 2; y

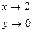
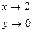
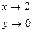
3. lim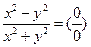

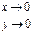x

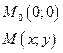
Будем стремить точку М к точке М_о по прямым у = кх.

Рассмотрим.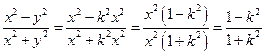

Давая k различные значения, будем получать различные значения данного выра­жения. Это означает, что предела не существует.

Опр.2 Функция z = f(x,y) называется непрерывной в точке (х_о,у₀) если она:

1. Определена в этой точке;

2. Существует lim f(x,y);

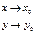
З. Этот предел равен значению функции в этой точке.

(Функция z = f(x,y) называется непрерывной в точке (х₀,у₀), если для любого ε>0 существует δ>0, что для всех точек М, удовлетворяющих неравенству выполнится неравенство .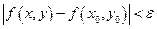

Если обозначить (х-х_о) = ∆х; (у-у_о) = ∆у, то соотношение можно записать в виде:.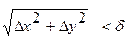

1.Сумма конечного числа непрерывных в точке 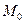функций есть функ­ция, непрерывная в этой точке.

2.Произведение конечного числа непрерывных в точке 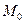функций
есть функция, непрерывная в этой точке.

3.Частное от деления конечного числа непрерывных в точке 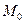функ­-
ций есть функция, непрерывная в этой точке, за исключением тех точек, в которых знаминатель обращается в 0.

4.Сложная функция, состоящая из непрерывных функций, есть функция, непрерывная в этой точке.

5.Если условие непрерывности не выполняется, то функция терпит разрыв.

Пример.

1. 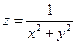; точка O (0;0) – точка разрыва.

2.

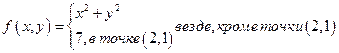
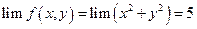
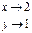
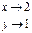
f (2, 1) = 7

Предел в точке (2, 1) существует, но он не равен значению функции в этой точке, значит (2, 1) – точка разрыва.

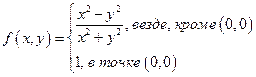
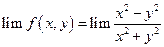не существует, значит (0,0) – точка разрыва

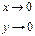
Частные производные функции двух переменных.

Графиком является некоторая поверхность.

Дадим х приращение ∆х, оставляя y постоянным. Функция получит приращение ∆_xz. Оно называется частным приращением функции по переменной х.

Опр. Если существует предел ,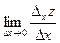

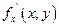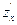то он называется частной производной от функции z = f(x,y) по переменной х и обозначается или или.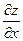

=

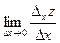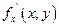
Аналогично:

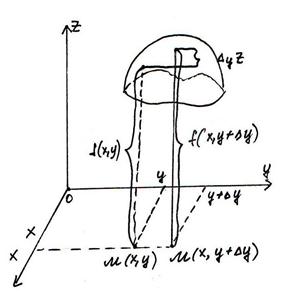
Дадим у приращение 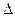у, оставляя х неизменным. Тогда функция получит приращение 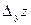- частное приращение функции по переменной у.

Опр. Если существует 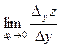, то он называется частной производной от функции z = f(x, y) по переменной y и обозначается ; ;

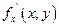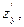
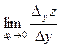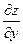
Геометрический смысл частных производных.

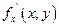
tgβ == =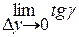

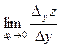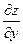
Итак, 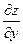есть тангенс угла наклона касательной к кривой, образованной пересечениями поверхности с плоскостью х = соnst, к оси ОУ.

Аналогично 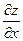- тангенс угла наклона касательной к кривой, образованной пересечением поверхности y = const, к оси ОХ.

Пример1.

Найти частную производную функции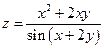

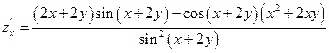
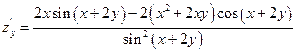
Пример 2.

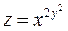
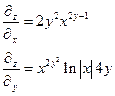
Пример 3.

U = Z^xy

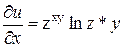
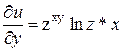
Полноеприращение функции. Дифференциируемость функции. Связь с непрерывностью.

z = f(x, y)

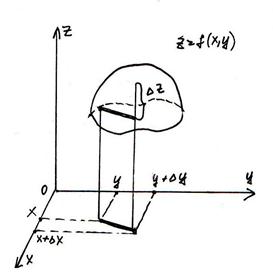
Дадим х приращение 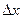, а у приращение 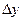. Функция получит приращение

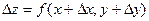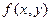- - полное приращение функции.

Теорема.

Если функция непрерывна в точке (х, у), то

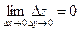
Доказательство:

Т.к. функция непрерывна в точке (х, у), то она определена в этой точке и существует

=

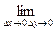
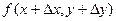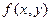
Перенесём всё в одну часть равенства:

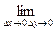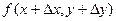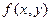(- ) = 0

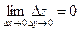
Обратно.

Если 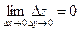, то функция 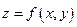непрерывна в точке (x, y).

Опр. Функция z = f(x,y) называется дифференцируемой в точке (х,у), если её пол­ное приращение представимо в ви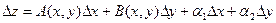де: , где 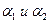- бесконечно малые функции более высокого порядка,чем 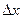и 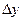, а А(х,у) и В(х,у)- заданные функции.

Пример.

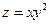
Теорема.

(Связь дифференцируемости с непрерывностью):

Если функция диффе­ренцируема в точке (х,у),то она непрерывна в этой точке.

Доказательство: Т.к. функция дифференцируема в точке (х,у), то её полное при­ращение представимо в ви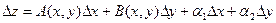де:

, где 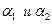бесконечно малые функции при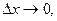 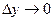Перейдём в этом равенстве к пределу

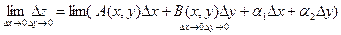
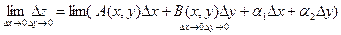= 0

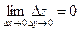. Это означает, что z = f(x, y) непрерывна.

Теорема.

(Необходимое условие дифференцируемости функции двух переменных):

Если функция дифференцируема в точке (х, у),то в этой точке у неё существует частная производная f'_x (x,y) и .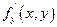

Доказательство: Т.к. функция дифференцируема в точке (х, у), то её полное при­ращение представимо в виде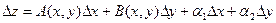. Положим в этом равенстве 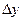=0. Тогда . Разделим обе части на :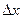

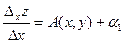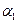, где - бесконечно малая при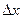 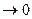. Перейдём в этом равенстве к пределу:

Т.к. функция А (х,у) известна (т.е. существует), значит предел левой части тоже существует, но

=

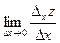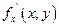
Значит 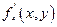существует.

Аналогично:

Пусть 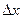= 0, разделим обе части на 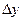: тогда,

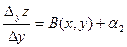где 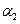- бесконечно малая при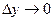

Перейдём в этом равенстве к пределу:

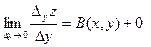
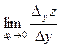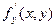= . Значит 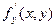существует.

Т.о.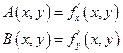

Замечание:

Функция дифференцируема в точке (x, y), если ее полное приращение представлено в виде:

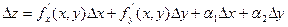, где 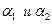бесконечно малые функции при ,.

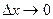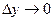Теорема.

(Достаточное условие дифференцируемости)

Если в окрестности точки (х, у) функция z = f(x,y) имеет частные производные и эти производные непрерывны в этой точке, то функция z = f(x,y) дифференцируема в этой точке.

Доказательство: Дано: производные 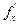и f'_y существуют, они непрерывны в точке (х,у). Рассмотрим полные производные функции: =()

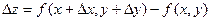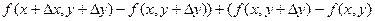Первая разность есть приращение функции одной переменной х при изменении х от х до (). По теореме Лагранжа для функции одной переменной 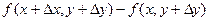=, где 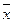лежит между х и ().

Аналогично.

Вторая разность есть приращение функции одной переменной у при изменении у от у до . По теореме Лагранжа: 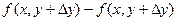, где у лежит между у и.

Тогда 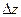будет записано: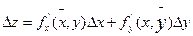

Т.к. 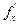и f'_y непрерывны в точке (х,у), то по определению непрерывности: =

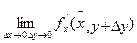Аналогично.

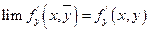
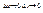
По теореме о бесконечно малых функциях

получим: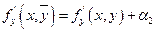

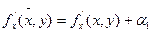
где 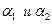бесконечно малые функции при ,..

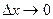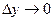Подставим, тогда: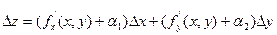

Раскроем скобки: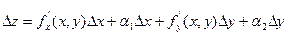

Это означает, что функция дифференцируема в точке (x, y).

Производная сложной функции.

1 случай.

Даны функции 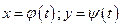и функция z = f(x,y).

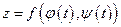- сложная функция, зависящая от t.

Теорема.

Если функции 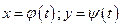дифференцируемы в точке t, а функция 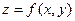дифференцируема в точке (x, y), где 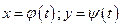, то сложная функция 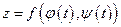дифференцируема в точке t и ее производная находится по формуле:

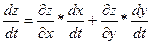
Доказательство:

Дадим переменной t приращение 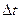, тогда функции 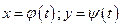получат приращение 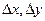. Тогда функция z = f(x, y) (функция двух переменных) получит полное приращение 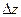. Т.к. функция z = f(x,y) дифференцируема в точке (х, у) то её полное приращение представимо в ви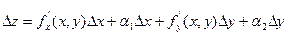де: , где 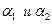бесконечно малые функции при ,.

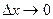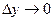Разделим это равенство на :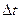

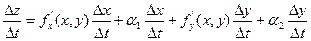
Перейдём в этом равенстве к пределу: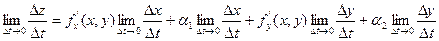

т.к. функции 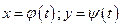дифференцируемы в точке t, то существует =

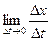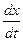
Аналогично =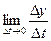

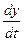
Т.к. 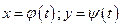дифференцируемы в точке t, то они непрерывны в этой точке, т.е. при ,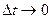

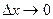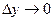
Поэтому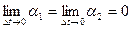

Т.о. получаем: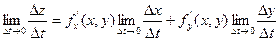

Правая часть существует, значит существеут =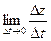

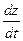
Т.о. получаем, что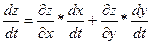

Пример.

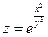, где .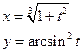

Случай 2.

Теорема.

Пусть x = x(u, v) и y = y(u, v), z = f(x(u, v), y(u, v)) – сложная функция двух переменных u и v.

Теорема.

Если сложные функции x = x(u,v) и y = y(u,v) дифференцируемы в точке (u,v), а функция z = f(x,y) дифференцируема в точке (х, у), где x = x(u,v) и y = y(u,v), то сложная функция z = f(x(u,v), y(u,v)) дифференцируема в точке (u,v) и её частная производная находится по формуле:

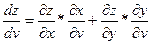
Доказательство:

Дадим переменной u приращение 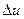, оставив v неизменной. Тогда x = x(u,v) получит приращение 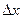, а функция y = y(u,v) получит приращение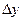. Тогда функция z = f(x,y) получит полное приращение 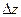. Т.к. функция z = f(x,y) дифференцируема в точке (х,у), то её приращение представимо в ви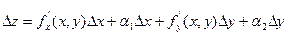де:

, где 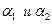бесконечно малые функции при ,.

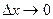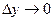Разделим это равенство на :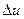

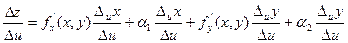
Перейдём в этом равенстве к пределу при :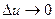

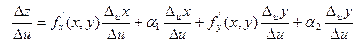
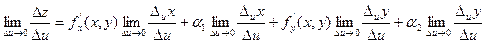Т.к. функции x = x(u,v) иy = y(u,v) дифференцируемы в точке (u,v), по необходимому условию дифференцируемости функции в этой точке у них существуют частные производные 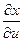и . Т.е. существует =, =

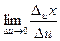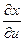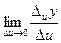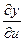
Т.к. функции x = x(u,v) иy = y(u,v) дифференцируемы в точке (u,v), то эти функции непрерывны в точке (u,v), а это значит, что:

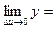0, 0 при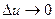

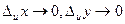
Тогда 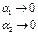, т.е.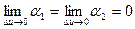

Т.о. получаем, что

Но 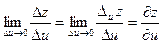для функции z = f(x(u,v), y(u,v)). Т.к. правая часть существует, то существует и предел левой части, равной 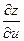. Т.о. получаем: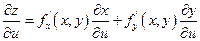

Или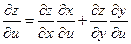

Аналогично доказывается и второе равенство теоремы.

Пример 1.

Дана функция: , где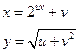

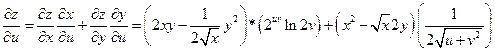
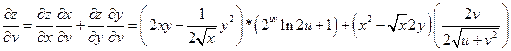
Пример 2.

Дана функция: 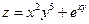, где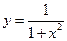

;

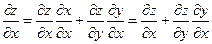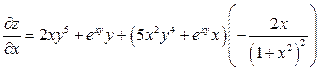
Дифференциал функции двух переменных.

Дана функция z = f(x,y) дифференцируемая в точке (х, у). Тогда её полное приращение представимо вви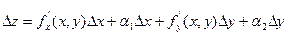де: , где 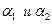бесконечно малые функции при ,.

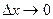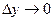В этом приращении различают две части:

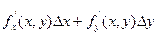- главная часть приращения функции,

а 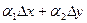- бесконечно малые более высокого порядка, чем 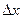и .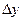

Опр. Главная часть полного приращения функции называется дифференциалом функции и обозначается dz.

Итак, по определению: dz =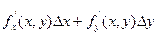или 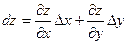(1-ая формула дифференциала).

Если отбросить бесконечно малые болле высокого порядка, то .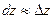

-

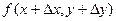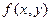
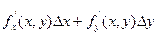
Отсюда найдём: (формула для приближённых вычислений)

+

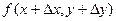
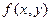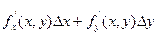
Пример: вычислить

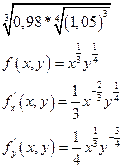
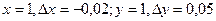
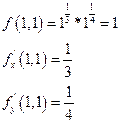
Инвариантность формы дифференциала.

Было установлено, что 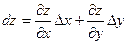. Рассмотрим функцию z = x, тогда с одной стороны dz = dx,а с другой по определению дифференциала 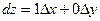. Отсюда 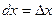. Аналогично рассмотрим фунуцию z = y, с одной стороны dz = dy, a с другой 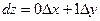, поэтому 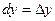. Тогда дифференциал запишется в виде: 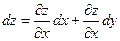(2-ая форма дифференциала). Эта форма дифференциала не зависит от того, является ли х и у независимыми переменными или некото­рыми функциями от других переменных. Покажем это. Формулу мы вывели в предположении, что x и y независимые переменные. Предположим теперь, что

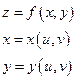
Тогда сложная функция 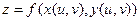от переменных u и v. В этом случае u и v – независимые переменные, x и y – промежуточные. Тогда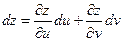

По правилу дифференцирования сложной функции найдем

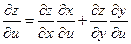
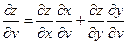
Подставим в дифференциал: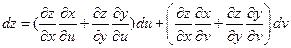

Раскрывая скобки и группируя, получим: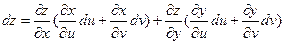

Но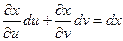

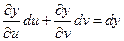
Тогда получаем:

Формула дифференциала применима в том случае, если x и y независимые переменные, и если они являются функциями.

Производная неявной функции.

Опр. 1 Если каждому значению x ставится в соответствие те значения y, для которых имеет место равенство F (x, y) = 0, то говорят, что это равенство определяет y как функцию от х, заданную неявно.

Пример

1)

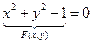
Разрешим это неравенство относительно у:

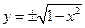
2)

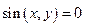
если 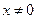, то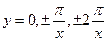

если х = 0, то у – любое значение.

Замечание

Не всякое уравнение определяет неявную функцию:

Теорема существования неявной функции:

Если 1) F (x, y) определена и непрерывна вместе со своими частными производными 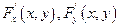в окрестности точки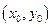

2)

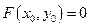
3) 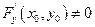, то:

1. уравнение F (x, y) = 0, в прямоугольнике

<<, <<

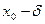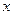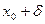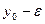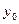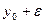
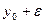
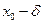
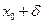
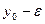
Определяет у, как однозначную и непрерывную функцию оси х.

2. При и .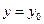

3. Эта функция f (х) дифференцируема в интервале 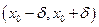и ее производная находится по формуле .

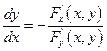Покажем, что имеет место последнее равенство. Для этого продифференцируем равенство

F (x, y) = 0 по правилу дифференцирования сложной функции, считая у – функцией от х.

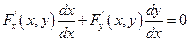
Так как по теореме существования 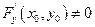и ввиду непрерывности этой функции, то в окрестности точки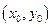 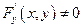. Тогда: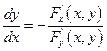

Пример

Задана неявная функция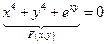

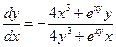
Опр. 2 Если каждой паре чисел (х, у) ставятся в соответствие те значения z, для которых ваполняется равенство F (x, y, z) = 0, то говорят, что это уравнение определяет z как функцию от x, y, заданную неявно.

Пример.

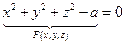
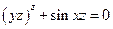
Если функция F(x,y,z) определена и непрерывна вместе со своими частными производными F'_x(x,y,z), F'_y{x,y,z), F'_z(x,y,z) в некоторой точке 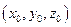, и при этом 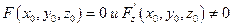, то это равенство определяет z как функцию от х,у (т.е. эта функция существует) и её частная производная находится по формулам:

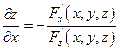
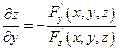
Покажем это: равенство F'(x,y,z) = 0 продифференцируем по х, считая у постоян­ным по правилу дифференцирования сложных функций.

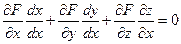
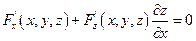
Отсюда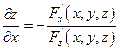

Аналогично дифференцируя равенство F(x,y,z) = 0 по у, считая х постоянным по правилу дифференцирования сложных функций, получаем:

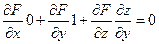
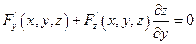
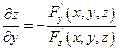
Пример 1.

Функция задана уравнением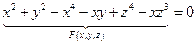

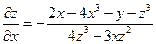
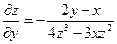
Пример 2.

Показать, что функция z, определяемая уравнениями F(x-az;y-bz) = 0, где F - произвольная дифференцируемая функция своих аргументов удовлетворяю­щих условию:

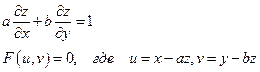
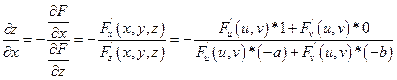
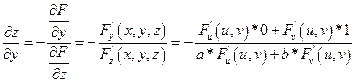
Подставим в уравнение:

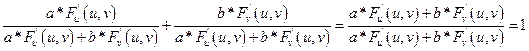
Частные производные высших порядков.

Дана функция z = f(x,y), дифференцируемая в точке (х,у). Значит у неё существуют частные производнаые 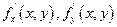. Они являются снова функциями двух переменных,и если они дифференцируемы в точке (х,у), то от каждой из них также существуют частные производные. Всего их 4 и они называются частными производными второго порядка и обозначаются: 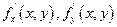или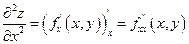

Смешанные производные второго порядка:

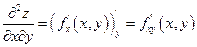
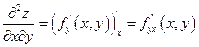
Производные третьего порядка:

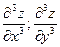
Смешанные производные третьего порядка:

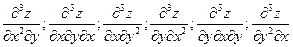
Пример.

Найти производные третьего порядка функции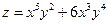

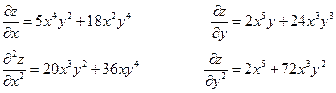
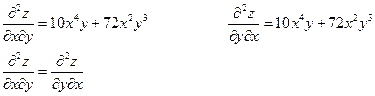
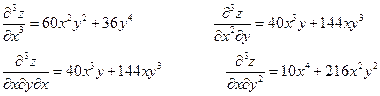
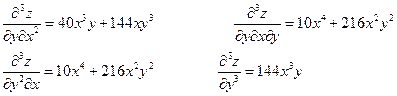
Вывод: Смешанные производные, отличающиеся только последо­вательностью дифференцирования, равны.

Дифференциалы высших порядков

Дана функция z=f(x,y), дифференцируемая в точке х. Было ранее установлено, что

dz=f_x’(x,y)dx+f_y’(x,y)dy,где х и у независимые переменные.

Зафиксируем dx и dy.

Опр. Дифференциалом второго порядка называется дифференциал от дифферен­циала первого порядка и обозначается:

d² z=d(dz)=d(f_x(x,y)dx+f_y(x,y)dy)=d(f_x’(x,y)dx)+d(f_y’(x,y)dy)=

=d(f_x’(x,y))dx+d(f_y’(x,y))dy=((f_xx’’(x,y))dx+(f_xy’’(x,y))dy)dx+(f(_yx’’(x,y)dx+f_yy’’(x,y)dy)dy=f_xx’’(x,y)dx²+2f_xy’’(x,y)dxdy+f_yy’’(x,y)dy²

d²z=f_xx’’(x,y)dx²+2f_xy’’(x,y)dxdy+f_yy’’(x,y)dy²

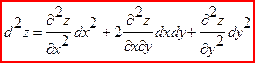
Дифференциал третьего порядка

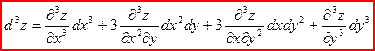
Символически дифференциалы различных порядков можно записать следующим образом:

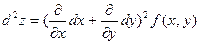
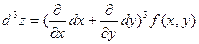
Замечание Дифференциалы высших порядков свойством инвариантности не обладают. Рассмотрим dz=f_x’ (x,y)dx+f_y’ (x,y)dy,где х и у являются некоторыми функциями

от других переменных. В этом случае dx и dy фиксировать нельзя. Тогда

d²z = d(dz)=d(f_x’(x,y)dx + f_y’(x,y)dy) =

= d(f_x’(x,y)dx)+ d(f_y’(x,y)dy) = {по свойству дифференциалов, что d(u ^.v)=v^.du+u^.dv}= d(f_x’(x,y))dx + f_x’(x,y)d(dx)+d(f_y’(x,y))dy+f_y’(x,y)d(dy) =

(f_xx’’(x,y)dx+f_xy’’(x,y)dy)dx+fx’(x,y)d²x+(f_yx’’(x,y)+f_yy’’(x,y)dy)dy+f_y’(x,y)d²y=

=f_xx’’(x,y)dx²+2f_xy’’(x,y)dxdy+f_yy’’(x,y)dy²+f_x’(x,y)d²x+f_y’(x,y)d²y

Форма дифференциалов изменилась.

Пример. Найти дифференциал второго порядка z=ln(x³+y²)

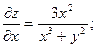
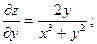
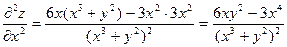
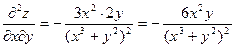
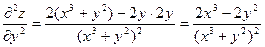
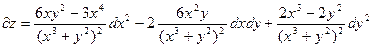
Касательная плоскость и нормаль поверхности

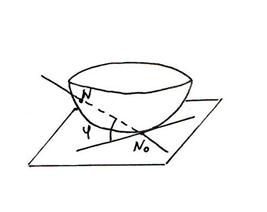Дана функция z=f(x,y), дифференцируемая в точке N₀(x_0,,y_0,,z₀). Графиком её является некоторая поверхность.

Опр. Касательной плоскостью поверхности z=f(x,y) d в точке N_o, называется плоскость, для которой угол между этой плоскостью и секущей N_oN стремится к нулю при стремлении точки N к N_o по поверхности.

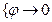при ;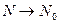

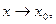
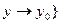
Касательная плоскость либо существует в точке, либо не существует.

Например, возьмём поверхность:

;

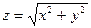
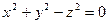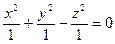
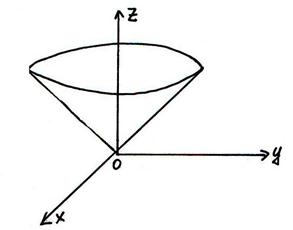в точке (0,0,0) касательная к плоскости не существует, т.к.: ;

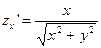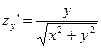
Частные производные в точке (0,0,0,) не существуют, значит функция не дифференцируема в этой точке.

Пусть функция дифференцируема в точке (x₀,y₀). Покажем, что плоскость, заданная уравнением z-z₀=fx’(x₀,y₀)(x-x₀)+fy’(x₀,y₀)(y-y₀) является касательной поверхностью.

Дадим 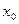и 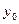приращения 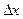и .

=

=

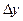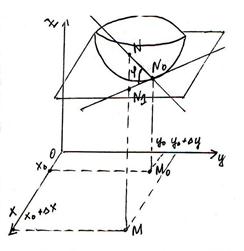
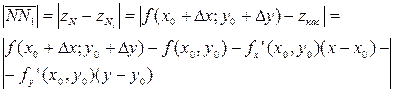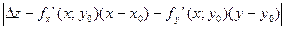
Известно, что т.к. функция дифференцируема, то ее точное приращение представимо в виде:

,

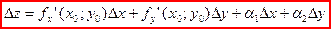где - бесконечно малые при 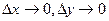т.е. мы имеем, что: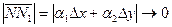при 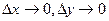т.е. при 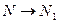, при этом 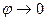. Значит, рассматриваемая плоскость является касательной.

Опр. Прямая, проходящая через точку касания перпендикулярно касательной плоскости, называется нормалью поверхности в данной точке.

Уравнение нормали

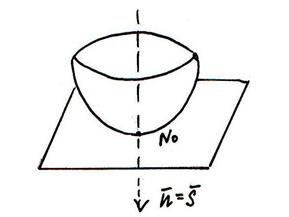Уравнение касательной перепишем в виде:

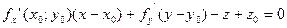
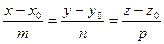
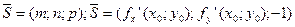
Тогда уравнение нормали запишется:

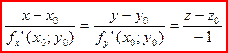
Пример. Написать уравнение касательной плоскости и нормали 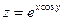в точке

с кооординатами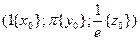

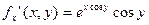
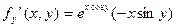
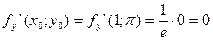
Уравнение касательной плоскости:

,

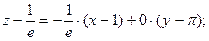
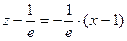Уравнение нормали:

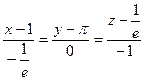
Уравнение касательной плоскости поверхности, заданной неявно

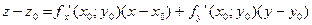
Поверхность задана неявно уравнением:

F(x,y,z)=0.

По правилу дифференцирования неявных функций известно, что:

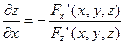и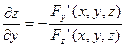

Тогда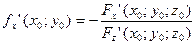

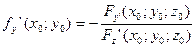
Подставим в уравнение:

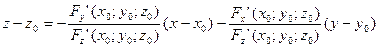{умножим на произведение и перенесем влево}

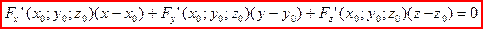
Уравнение нормали

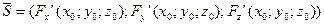
Пример. Написать уравнение касательной плоскости и норали к поверхности F(x,y,z), заданной неявно x(y+z)(xy-z)+8=0 в точке (2;1;3), которая лежит на поверхности.

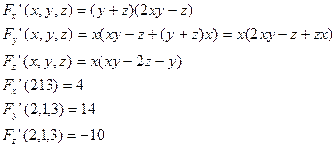
Уравнение плоскости:

4(x-2)+14(y-1)-10(z-3)=0; 2x+7y-5z+4=0

Уравнение нормали:

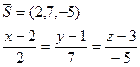
Дата добавления: 2014-01-04