Портфель с минимальным риском

Пусть целью инвестора является выбор портфеля с минимальным возможным риском, то есть необходимо так выбрать 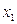и 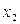, чтобы величина риска портфеля 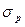была бы наименьшей. Эту задачу можно просто решить аналитически. Прежде всего, заметим, что для портфеля из 2-х активов всегда должно выполняться бюджетное ограничение

,

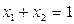- сумма долей равняется единице. Значение 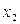мы можем выразить через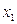

.

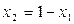Обозначим

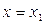
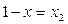
Задачу выбора портфеля с наименьшим риском можно записать

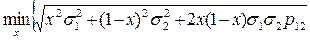(10.3)

Запишем условие первого порядка для данной задачи (возьмем про­изводную по х и приравняем ее к нулю)

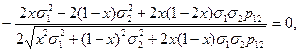
откуда, при условии, что знаменатель не равен нулю, получим

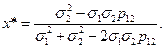(10.4)

Формула (10.4) дает возможность определить портфель, риск (стандартное отклонение доходности) которого минимален.

Рассмотрим некоторые частные случаи.

1. Пусть 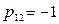тогда

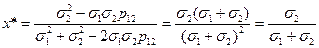
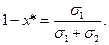
В этом случае риск портфеля равен нулю.

2. В случае, когда 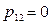, то есть какая-либо взаимосвязь между до­ходностью первого и второго актива отсутствует, портфель с наимень­шим риском выбирается так:

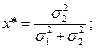
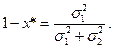
Стандартное отклонение такого портфеля будет равно 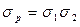. Есл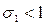и и 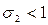, риск портфеля будет меньше, чем риск каждого из от­дельно взятых активов.

3. Когда 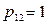, оптимальный портфель выбирается следующим обра­зом:

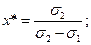
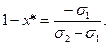
Риск такого портфеля также равен нулю:

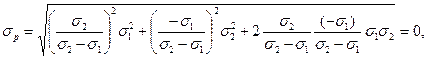
но существует важное отличие от случая, когда 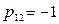: при совершен­ной отрицательной корреляции оптимальные объемы инвестиций в ка­ждый из активов были положительными. Здесь же, л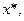ибо либо 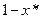меньше нуля (причем, если 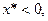то 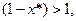и наоборот). Отрица­тельный объем инвестиций означает короткую продажу - когда прода­ется актив, взятый в долг с обязательством последующего возврата. Следовательно, в случае положительной корреляции, для того, чтобы получить портфель с минимальным риском, необходимо коротко про­дать один из активов, и инвестировать все имевшиеся и вырученные за счет короткой продажи средства во второй актив.

Дата добавления: 2014-01-04