Билинейное преобразование

Запишем формулу передаточной функции разомкнутой системы:

. (9.6)

Чтобы построить частотные характеристики необходимо сделать замену:

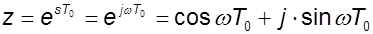. (9.7)

Для непрерывных систем границей устойчивости на s -плоскости является мнимая ось. А у дискретных систем – границей устойчивости на z -плоскости является единичная окружность. Однако с помощью билинейного преобразования единичная окружность на z -плоскости отображается в мнимую ось на w -плоскости. Применяем w -преобразование:

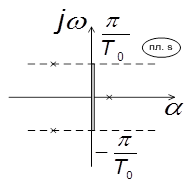
Рисунок 9.4 – Расположение полюсов на плоскости s

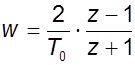; (9.8)

, (9.10)

где ,

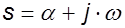, тогда 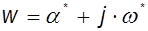. (9.11)

Для построения частотных характеристик принимаем , .

Найдем w, подставив :

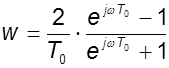, (9.12)

перейдем к половинному углу:

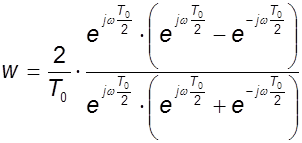, (9.13)

разложим и по формулам Эйлера:

(9.14)

при и – становится мнимой.

→ – абсолютная псевдочастота.

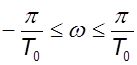
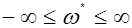
Рисунок 9.5 – Переход о плоскости s к плоскости

w -преобразование отображает отрезок мнимой оси от до 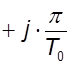в плоскости s во всю мнимую ось в плоскости w.

Пример 4:

Дана передаточная функция непрерывной части цифровой САУ.

.

Найдем передаточную функцию цифровой системы .

Находим

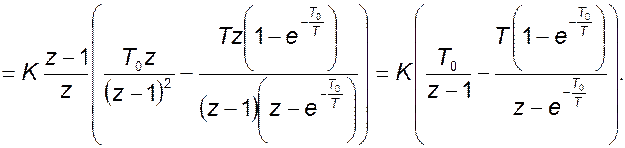Сделаем замену: .

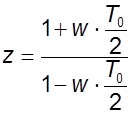Найдем передаточные функции отдельных составляющих

,

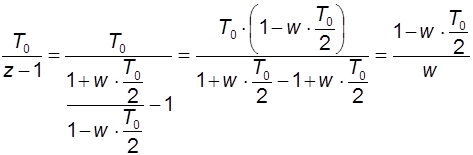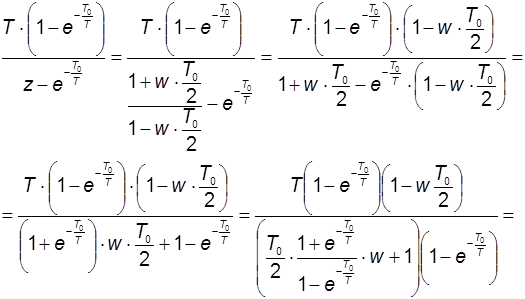
, где .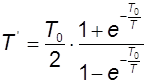

Найдем теперь передаточную функцию цифровой системы

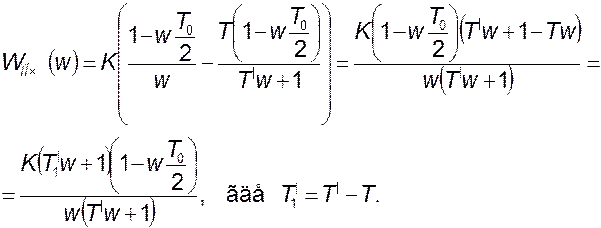
Логарифмические характеристики системы при 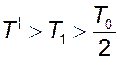приведены на рис. 9.6.

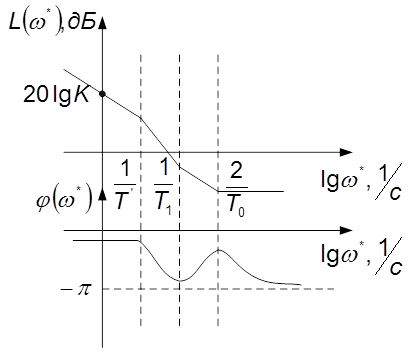Звено, имеющее нуль или полюс в правой полуплоскости, называется неминимально фазовым. Поэтому звено с передаточной функцией 1-го

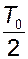
Рисунок 9.6 – Логарифмические характеристики

Пример 5:

Проверить устойчивость замкнутой импульсной системы с экстраполятором нулевого порядка; передаточная функция непрерывной части:

;

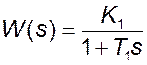К ₁=100, T ₁=0.1c, период квантования сигнала 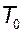=0.1c.

Решение. Передаточная функция разомкнутой импульсной системы равна:

.

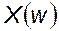
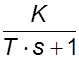
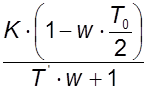
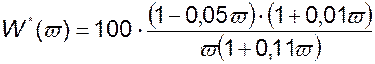Ей соответствуют логарифмические переходные характеристики (рис 8.10):

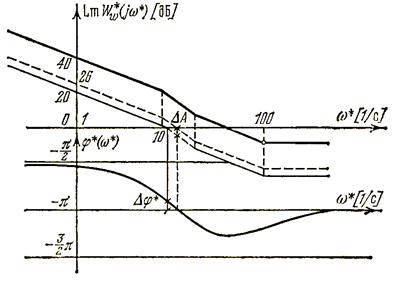
Рисунок 9.7 – Логарифмические характеристики системы

Из них видно, что рассматриваемая система неустойчива. При снижении коэффициента k ₁ до величин менее 26 дБ система становится устойчивой. При Lm (k ₁)=20 дБ (т. е. k ₁=10) запасы системы по амплитуде и по фазе составляют Δ А =6 дБ, Δ φ^*= 20 град.

Дата добавления: 2014-01-04