Атом гелия

Простейшим после атома водорода является атом гелия, электронная оболочка которого состоит из двух электронов. Однако, несмотря на относительную простоту атома гелия, попытки построить его теорию в рамках старой теории Бора не увенчались успехом. В дальнейшем стало ясно, что старая теория Бора в принципе не могла дать решение проблемы атома гелия. Это обусловлено двумя обстоятельствами. Во-первых, теория Бора не позволяет учесть обменной энергии, существование которой является чисто квантовым эффектом. Во-вторых, теория Бора не учитывает наличие спина у электрона.

Теория многоэлектронных атомов в квантовой механике не встречает принципиальных трудностей, хотя практические вычисления весьма сложны и громоздки. В простейшем случае атома гелия, если не учитывать спины, задача сводится к решению уравнения Шредингера с двумя электронами. Полная энергия системы слагается из следующих частиц:

а) кинетических энергий обоих электронов;

б) потенциальных энергий обоих электронов в одном и том же поле ядра атома;

в) энергии взаимодействия между электронами: .

Волновая функция при этом зависит от координат обоих электронов, то есть шести переменных.

Таким образом, получаем следующее уравнение Шредингера для определения волновой функции :

(8.2)

Через ,обозначены радиусы-векторы первого и второго электронов. Ядро атома в рассматриваемом приближении считается неподвижным и принимается за начало координат. Точное решение этого уравнения- очень сложная задача.

Такая задача решается с помощью теории возмущений, Которая использует тот факт, что энергия взаимодействия каждого из электронов с ядром больше, чем энергия взаимодействия электронов друг с другом. Поэтому в нулевом приближении можно пренебречь энергией взаимодействия.

Поскольку взаимодействие между электронами не учитывается, каждый из электронов считается движущимся в поле ядра совершенно не зависимо от движения другого электрона. Значит энергия двух электронов равна сумме энергий электронов:

(8.3)

-где - энергия первого электрона, находящегося в состоянии , - энергия второго электрона находящегося в состоянии .

Учитывая, что функция 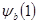независима от , получаем два уравнения:

(8.4)

Это есть уравнение движения электрона в кулоновском поле ядра. Решение этих уравнений, а значит и энергетические уровни каждого из электронов совпадают с энергетическими уровнями водородоподобного атома.

Однако такая сравнительно простая картина существенно изменяется, если принять во внимание взаимодействия электронов и их спины.

Волновая функция

(8.5)

представляет решение уравнения Шредингера (8.2) с собственным значением энергии . Очевидно, что из-за идентичности электронов ничего не изменится, если электрон 2 поместить в состояние , а электрон 1- в состояние . Таким образом, наряду с функцией (8.5) решением уравнения (8.2), также будет функция

(8.6)

принадлежащая тому же собственному значению , то есть имеются две волновые функции, принадлежащие одному и тому же собственному значению. Другими словами собственное значение энергии вырождено, что является результатом тождественности электронов. Такое вырождение называется обменным.

Из-за идентичности электронов и возможности их обмена между состояниями и . Благодаря чему каждый из электронов как бы находится частично в состоянии и частично в состоянии . Между ними возникает дополнительное взаимодействие, которое называется обменным. А соответствующая энергия – обменной энергией.

Обменная энергия не имеет классического аналога и является чисто квантовым эффектом.

Таким образом, полная энергия атома 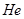с учетом взаимодействия частиц будет выглядеть

(8.7)

-где С – член, характеризующий кулоновскую энергию взаимодействия

электронов

А – член, характеризующий обменную энергию взаимодействия, знак

которой определяется ориентировкой спинов.

Здесь возможны два варианта:

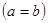(8.8)

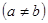(8.9)

Первое уравнение соответствует случаю, когда оба электрона находятся в основном состоянии , их полная энергия равна 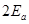. Согласно принципу Паули, в этом случае они должны обладать противоположно направленными спинами. Тогда суммарное спиновое число . Такой энергетический уровень есть синглетным, а гелий, который находится в таком квантовом состоянии, называется парагелием. Это электронная конфигурация .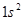

Благодаря взаимодействию электронов синглетный уровень сдвигается на величину, равную кулоновской энергии взаимодействия.

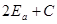
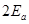
пусть теперь один из электронов находится в основном состоянии , а второй электрон – в возбужденном состоянии . Тогда без учета взаимодействия полная энергия есть . Этот энергетический уровень вырожден благодаря наличию обменного выражения: имеются синглетное и триплетное состояние двух электронов с одной и той же энергией. Однако при учете взаимодействия электронов обменное выражение снимается – триплетное состояние (характеризуется отрицательной обменной энергией) имеет меньшую энергию, чем синглетное (характеризуется положительной энергией)

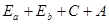
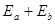
Гелий, находящийся в таком квантовом состоянии, называется ортогелием, (то есть такой, у которого спин второго электрона совпадает по направлению со спином первого). Ближайшее по энергии допустимое принципом Паули состояние второго электрона есть . Таким образом, электронная конфигурация ортогелия - .

Многоэлектронные атомы. Метод самосогласованного поля.

Метод теории возмущений подходит лишь к атомам с небольшим количествам электронов. При увеличении числа электронов используют метод Хартри, который основан на замене электрического поля ядра и всех электронов, кроме одного выделенного, некоторым самосогласованным полем, в котором движется один электрон.

Исходными здесь являются волновые функции отдельных электронов без взаимодействия. С их помощью вычисляется потенциал, действующий на отдельные электроны. С этим потенциалом, как известным. Решается уравнение Шредингера для каждого электрона, и находятся новые волновые функции. С их помощью определяется уточненный потенциал и затем с этим потенциалом для каждого электрона решается уравнение Шредингера, и находятся следующие волновые функции. По мере приближения к точному решению различия между исходными и конечными функциями на каждом этапе сглаживаются. Согласование состоит в том, что с одной стороны, волновые функции отдельных электронов формируются согласованным полем; с другой стороны, самосогласованное поле само зависит от вида волновых функций электронов.

Векторная модель атома.

В атоме с двумя и более электронами орбитальные и спиновые моменты всех его электронов могут складываться двумя способами. Первый способ осуществляется, когда взаимодействие орбитальных моментов и электронов и спиновых моментов и друг с другом сильнее, чем взаимодействие и . Связь орбитального и спинового момента в этом случае называется слабой связью. Она является наиболее распространенной в легких атомах. Векторы орбитального и спинового моментов электронов складываются в этом случае порознь, образуя вектор суммарного орбитального момента атома:

;

и вектор суммарного спинового момента атома

; .

Оба суммарных момента складываются в суммарный полный момент атома:

; .

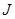Ввиду различной возможной ориентации векторов и квантовое число принимает следующие значения: , , … .

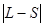Второй способ сложения орбитальных и спиновых моментов атомных электронов осуществляется, когда взаимодействие и для каждого из электронов сильнее, чем взаимодействие порознь орбитальных и спиновых моментов различных электронов между собой. Связь моментов атомных электронов в этом случае называется сильной связью. Эта связь существует преимущественно в тяжелых атомах. Векторы орбитального и спинового моментов каждого электрона атома складываются, давая вектор полного момента электрона: .

Суммарный полный момент атома образуется сложением полных моментов каждого из электронов

; .

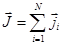Дата добавления: 2014-01-04