Со случайной ошибкой или неопределенностью значительно сложнее

Природа случайных ошибок и неопределенностей

Математический характер систематической ошибки элементарен, и нет необходимости ее рассматривать. Систематическая ошибка устраняется калибровкой или ремонтом. Наличие систематической ошибки и возможные последствия всегда можно предсказать

Если известно, что существует случайная ошибка, никогда нельзя установить ее абсолютную величину, произведя единственное измерение. Для исследования случайных ошибок, возникающих при проведении эксперимента, необходимо знать некоторые разделы математической статистики и теории вероятностей.

Необходимо измерить неизвестную величину, например длину жесткого стержня. Записывая каждое измерение, замечаем, что между отсчетами наблюдателей А, В, С и т. д. существуют некоторые отклонения. После того как все большее и большее число наблюдателей зафиксирует свои результаты, получаем выборку из некоторой генеральной совокупности. Рассмотрим небольшие равные интервалы длиной DХ и подсчитаем число отсчетов, попадающих в каждый из этих интервалов. Если теперь построить график зависимости средних значений Х для каждого интервала DХ от числа отсчетов, попадающих в каждый интервал, то получим гистограмму, аналогичную изображенной на рис.3

Чем больше отсчетов будет снято, тем меньший интервал DХ можно взять, и в пределе получим некоторую плавную кривую распределения.

Здесь рассматривается лишь одно распределение — нормальную кривую ошибок, часто называемую распределением Гаусса:

Рис.3.Гистограмма, полученная при измерении длины жесткого стержня.

Формула распределением Гаусса выводится на основе двух допущений: 1. Окончательная ошибка любого измерения представляет собой результат большого числа очень малых ошибок, распределенных случайным образом. 2. Положительные и отрицательные отклонения относительно истинного значения равновероятны.   Здесь: у — частота появления некоторого отклонения х относительно точного значения mх; y0 — частота появления нулевого отклонения, h — некоторая постоянная, характеризующая данное нормальное распределение, называемая модулем или показателем точности

Полагая, что y ₀ и h — постоянные, и строя зависимость у от х, получают хорошо знакомую колоколообразную кривую, изображенную на Рис.4.

Рис.4. Кривая плотности нормального распределения показаний измерительного прибора

Функция (2.1) и ее кривая непрерывны, т.е. они описывают совокупность, содержащую бесконечное множество измерений. Это так называемая генеральная совокупность, из которой для исследования берутся некоторые конечные выборки. Генеральная совокупность охватывает все множество отклонений для данного прибора. Нас интересует прежде всего математическое выражение для площади A под кривой. Площадь находится путем интегрирования из следующего выражения:

Интеграл можно вычислить, либо найти в таблице интегралов. Площадь равна:

Относительная частота появления событий – это вероятность события. Вероятность пояления всех событий равна 1. Поэтому площадь принимают равной единице. Тогда: и

.

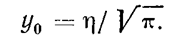В результате такого нормирования формула (2.1) принимает следующий вид:

у не является величиной, удобной для практического использования, необходимо знать вероятность появления отклонения любой данной величины.

Вероятность Р появления отклонения, лежащего в интервале от –х до +х, равна площади под кривой нормального распределения, ограниченной интервалом ±х, как показано на фиг.5. Математически эта вероятность выражается формулой:

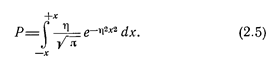
Дата добавления: 2014-01-04