Уравнение для энергетического спектра электронов

В частном случае, когда

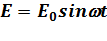, (11.11) можно считать, что симметричная часть ФР f₀ состоит из двух частей: основной, медленно меняющейся со временем благодаря неупругим столкновениям и постепенному набору энергии от поля (влияние второго члена в правой части уравнения (11.9)), - и поправки, связанной с влиянием первого члена. Так как f₁ ~ E₀, то этот член ~ (E₀)² и осциллирует с частотой приложенного поля. Средняя величина этого члена и определяет темп набора энергии от поля. Поскольку эти быстрые осцилляции не существенны для формирования энергетического спектра, при решении уравнения используют усредненные за период значения á f₀ ñ и á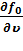ñ, т.е. пренебрегают “мелкими” вариациями ФРЭ в течение периода и считают, что она заметно изменяется в течение многих периодов.

Поэтому при интегрировании уравнения (11.10) мы подставим усредненную за период производную á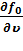ñ. В результате получим линейное уравнение

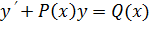, (11.12) которое решается методом интегрирующего множителя

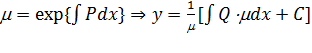. (11.13)

В нашем случае

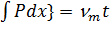, (11.14) а

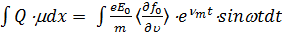. (11.15)

Решив систему (11.13-11.15), получим

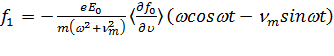. (11.16)

Введя обозначение

,

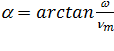Найдем решение для несимметричной части функции распределения

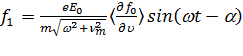. (11.17) Видно, что и осциллирует с частотой внешнего поля, но со сдвигом по фазе на угол a. В пределах высоких частот 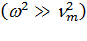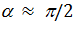. Тогда 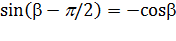и

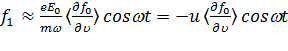, (11.18) где 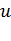- амплитуда колебательной скорости электрона в осциллирующем поле

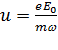. (11.19) Поскольку 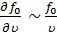, где u - характерная скорость теплового движения, получим в высокочастотном пределе оценку для :

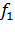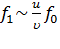. (11.20)

В пределах низких частот 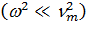сдвиг по фазе мал, и мы имеем

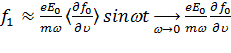. (11.21)

Последнее выражение можно сразу получить из уравнения (11.10), положив 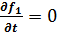. Асимптотическое значение 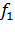, устанавливающееся через одно столкновение в пределе 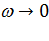, есть

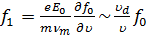, (11.22) где 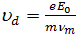представляет собой абсолютную величину дрейфовой скорости электрона. Выражения (11.20) и (11.22) определяют критерии малости 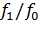поправки к симметричной ФРЭ, которое можно сформулировать так:

Асимметрия функции распределения электронов по скоростям может считаться малой, если амплитуда скорости колебаний электрона в переменном поле или дрейфовая скорость в постоянном поле малы по сравнению со средней тепловой скоростью электрона.

Дата добавления: 2014-01-04