
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 32. Признаки обратимости операторов. Теорема Рисса об общем виде линейного ограниченного функционала в гильбертовом пространсчве. Теорема Хана-Банаха
|
|
|
|
Утверждение 32.1 Если есть X, Y, Z – банаховы пространства,  L (X,Y),
L (X,Y),  L (Y,Z) - обратимые. Тогда оператор
L (Y,Z) - обратимые. Тогда оператор  (X,Z) обратим и
(X,Z) обратим и 
Док-во:
 явл. правым обратимым к
явл. правым обратимым к 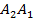 .
.
 – левый обратный
– левый обратный 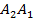 .
.
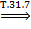 Ч.т.д.
Ч.т.д.
Утверждение 32.2 Пусть X, Y – банаховы пространства, 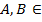 L (X,Y), А – обратим;
L (X,Y), А – обратим; 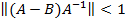 . Тогда оператор В тоже обратим.
. Тогда оператор В тоже обратим.
Док-во:

 и
и 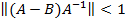 =>
=>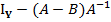 – обратим.
– обратим.
А – обратим  В – обратим.
В – обратим.
Оценки
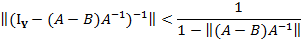
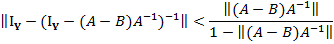

10. 
 =>
=>
20.  . Ч.т.д.
. Ч.т.д.
Замечание: Неравенство 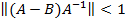 заведомо выполн., если выполн.
заведомо выполн., если выполн. 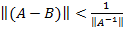 .
.
Это означ., что в L (X,Y) мн-во всех обратимых операторов явл. открытым, т.к. каждый оператор, попавший в шар В(А,  ) сост. из обратимых операторов.
) сост. из обратимых операторов.
Замечание: Если А обратим, 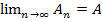 в L (X,Y), тогда начиная с N
в L (X,Y), тогда начиная с N 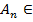 В(А,
В(А,  )=> все
)=> все 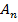 -обратимы =>
-обратимы => 
=> операция нахождения обратного оператора явл. непрерывной.
Утверждение 32.3 Пусть Н – гильбертово прост-во, 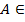 L (Н),
L (Н),  - ортонормир. базис прост-ва Н, сост.из собств. вект. оператора А, отвеч. соотв. собств. знач. λ k, т.е. выполн. А
- ортонормир. базис прост-ва Н, сост.из собств. вект. оператора А, отвеч. соотв. собств. знач. λ k, т.е. выполн. А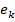 =λ k
=λ k 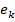
A обратим <=> 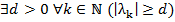 .
.
Док-во:
необходимость: Утв.31.2. => если А обратим, то 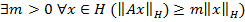
Пусть  , тогда
, тогда  .
.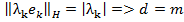 . Ч.т.д.
. Ч.т.д.
достаточность:  Ax=y
Ax=y
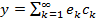 , где
, где  = < y,
= < y, 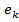 >
>
 ,
, 
 .
.
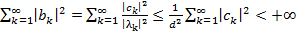 (т.к. y
(т.к. y 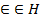 )
)

 A - обратим.
A - обратим.
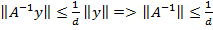 . Ч.т.д.
. Ч.т.д.
Опр.32.4 Пусть (Х, ) – нормир. прост-во, тогда L (X, K) наз. сопряж. к X прост-вом и обозн. X*.
) – нормир. прост-во, тогда L (X, K) наз. сопряж. к X прост-вом и обозн. X*.
Т 32.5 (Риса) Пусть Н - гильб. прост-во, тогда Н* изометрично Н. (Н* Н), т.е.
Н), т.е. 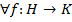 – лин.огр.
– лин.огр.  .
.
Док-во:
единственность: 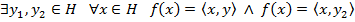

Пусть  =>
=> 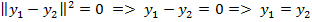 .
.
Докажем, что если  , то
, то 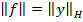
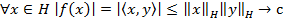 => f огр.
=> f огр. 
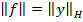 .
.
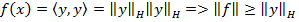 =>
=> 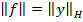 .
.
сушествование: 
Рассм. L =Ker f(x) = 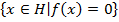 - векторное подпр-во Н.
- векторное подпр-во Н.
Докажем, что L замкн.
 - предельн. т. L.
- предельн. т. L.

 L,
L, 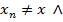
 .
.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 839; Нарушение авторских прав?; Мы поможем в написании вашей работы!