Существование и нахождение собственных значений и собственных векторов линейных операторов

Т е о р е м а 1. ПустьA =(a _ik) – матрица линейного оператора A в базисе e ₁, e ₂ ,…, e_n пространства V над полем P, l – переменная, принимающая значения в поле P. Тогда оператор A обладает собственными векторами тогда и только тогда, когда уравнение

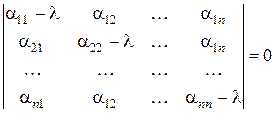. (5)

имеет, по крайней мере, один корень в поле P.

□ Þ Пусть x = b₁ e ₁+b₂ e ₂+…+b _ne_n – собственный вектор оператора A, т.е. A x = l₀ x для некоторого l₀ из поля P. Координаты g₁, g₂ ,…, g _n образа A x вектора x выражаются с помощью следующей системы равенств:

. (6)

Из равенства A x = l₀ x следует, что g _i =l₀b _i (i =1,2,…, n), и поэтому равенства (6) можно переписать в виде

, (7)

или после очевидных преобразований в виде

. (8)

Таким образом, арифметический вектор (b₁, b₂,…,b _n) является ненулевым решением однородной системы

. (9)

Но это возможно только в случае, когда определить этой системы равен 0, т.е.

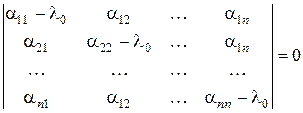. (10)

Последнее же равенство означает, что l₀ – корень уравнения (5).

Ü Обратно, если l₀ – корень уравнения (5), то выполнено равенство (10) и, следовательно, система (9) имеет ненулевое решение (b₁, b₂,…, b _n), т.е. выполнено равенство (8), а поэтому и равенство (7). Равенства (7) показывают, что координатная строка образа A x вектора x есть (l₀b₁, l₀b₂,…, l₀b _n). Это и означает, что для вектора x = b₁ e ₁+b₂ e ₂+…+b _ne_n имеет место равенство A x = l₀ x, т.е. x – собственный вектор оператора A. ◘

Из доказательства теоремы 1 вытекает

Следствие 1. Вектор x пространства V над полем P является собственным вектором оператора A, отвечающим собственному значению l₀, тогда и только тогда,когда его координатная строка является решением системы (8).

Определение 1. Многочлен | A– l E |, стоящий в левой части уравнения (5) называется характеристическим многочленом оператора A, а само уравнение | A– l E | =0 (5) называется характеристическим уравнением оператора A.

Учитывая определение 1, теорему 1 можно сформулировать следующим образом: оператор A тогда и только тогда обладает собственными векторами, его характеристическое уравнение имеет, по крайней мере, один корень в поле P.

Из доказательство теоремы 1 вытекает также

Следствие 2. Корнихарактеристического уравнения оператора A и только они являются собственными значениями этого оператора.

Доказательство теоремы 1 указывает

Дата добавления: 2014-01-04