Релятивистское динамическое уравнение. Закон преобразования сил

ЛЕКЦИЯ 17.

Если в динамическом законе движения частицы использовать физическую величину обычной классической силы, то динамическое уравнение для релятивистской частицы в СТО записывается в виде:

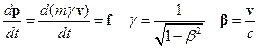(17.1)

Уравнение (1) имеет ньютонову форму второго закона динамики, с той лишь разницей, что в его правой части стоит трехмерный релятивистский импульс 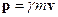. В правой части (1) стоит классическая сила 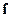, определяемая соответствующими законами, например, электромагнитная сила Лоренца

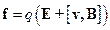
При наличии тангенциального ускорения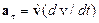, величина скорости изменяется со временем и классическое ускорение (т.е. ускорение, полученное по классическому рецепту как производная классической скорости по времени) оказывается не параллельным действующей силе

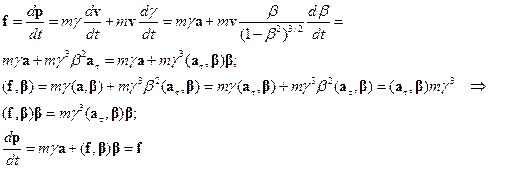(17.2)

В результате динамическое уравнение релятивистской частицы преобразуется к виду:

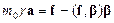(17.3)

Второе слагаемое в правой части уравнения (3) определяет плотность потока мощности действующей силы.

В случае, когда действующая на частицу сила ортогональна скорости частицы, имеем:

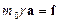(17.4)

В случае, когда действующая на частицу сила сонаправлена со скоростью частицы, имеем

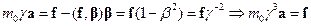(17.5)

Таким образом, если инерционность релятивисткой частицы по-прежнему связывать с ее массой, то приходится вводить две массы: поперечную 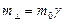и продольную массу .

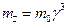Теорема об изменении кинетической энергии.

Из уравнения (1) находим

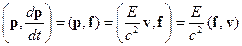(17.6)

С другой стороны, из закона сохранения энергии импульса частицы следует: 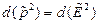, где 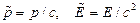приведенный импульс и приведенная энергия частицы. Тогда

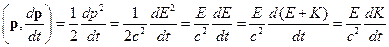
Сравнивая полученное выражение с уравнением (6), получаем уравнение для изменения кинетической энергии релятивистской частицы:

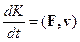(17.7)

Это уравнение полностью совпадает со своим классическим аналогом. Таким образом, изменение кинетической энергии релятивисткой частицы равно мощности действующей на нее силы.

Ковариантная форма динамического закона.

Поскольку интервал времени не является инвариантом преобразований Лоренца, классическая сила не является пространственной частью 4-х вектора, т.е. динамическое уравнение в ньютоновской форме не имеет ковариантного вида. Ковариантная форма уравнения означает, что в него входят только тензорные величины: скаляры, векторы, тензоры 2-го ранга и т.д. Поэтому ковариантную форму уравнения отождествляют с тензорной формой. Динамическому уравнению можно придать ковариантную форму, если вместо промежутка времени 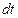использовать собственное время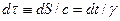(инвариант преобразований Лоренца), т.е. воспользоваться уже известным нам способом построения 4-х векторов. При этом изменение 4-импульса частицы вычисляется вдоль ее мировой линии. Таким образом, релятивистское динамическое уравнение в ковариантной форме имеет вид:

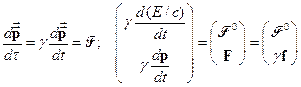
4- вектор 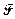называется силой Минковского. Его составляющие преобразуются при переходе из одной инерциальной системы в другую по формулам преобразований Лоренца (см. (16.3)). Пространственная часть этой силы 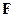связана с классической силой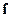и при переходе к классическому пределу переходит в последнюю: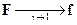. Рассмотрим физический смысл оставшейся (временнóй) компоненты 4-силы 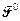, которая определяет изменение релятивистской энергии

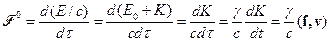
Следовательно, временная составляющая 4-х силы равна изменению кинетической энергии, вычисленному вдоль мировой линии частицы.

Классическая сила не является пространственной компонентой 4-вектора и не инварианта относительно перехода из одной инерциальной системы в другую. Найдем закон преобразования этой силы при таком переходе.

Разложим силу, действующую на частицу в данный момент времени, на две составляющие: параллельную и перпендикулярную мгновенной скорости:

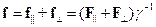
которым в классическом пределе соответствуют тангенциальная и нормальная составляющие ускорения. Перейдем в инерциальную систему , движущуюся относительно лабораторной системысо скоростью равной мгновенной скорости частицы в рассматриваемый момент времени

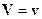
Будем называть такую систему сопутствующей. В этой системе классическая сила совпадает с релятивистской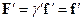, поскольку .

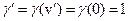Перейдем из сопутствующей системы 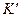в систему отсчета 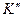, движущуюся относительно сопутствующей системы с произвольной скоростью 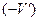. В этой системе, согласно релятивистскому правилу сложения скоростей, скорость частицы равна 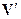. Согласно преобразованиям Лоренца, перпендикулярные относительной скорости компоненты 4-х силы остаются неизменными (так же как поперечные компоненты радиус-вектора мирового пространства). Следовательно, в новой системе 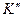, получаем

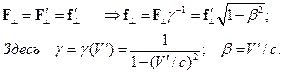
Таким образом, в разных инерциальных системах отсчета величина поперечной к скорости компоненты силы – разная. Максимальная сила имеет место в той системе, в которой в данный момент частица покоится (т.е. в сопутствующей системе). При приближении скорости частицы к световой поперечная компонента силы уменьшается до нуля .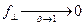

Рассмотрим продольную компоненту силы. Направим осии 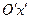в обеих системах 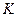и 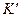вдоль направления мгновенной, и, следовательно, относительной скорости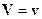. Заметим, что в сопутствующей системе временная компонента 4-х силы

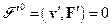
поскольку в этой системе частица в данный момент покоится. Перейдем из сопутствующей системы в систему отсчета 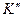, движущуюся относительно сопутствующей системы с произвольной скоростью 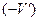. В этой системе согласно релятивистскому правилу сложения скоростей, скорость частицы равна 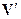. Тогда, согласно преобразованиям Лоренца, в новой системе 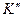, получаем

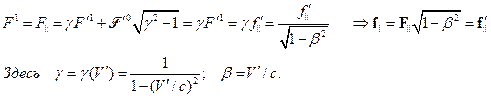
Продольная компонента силы во всех инерциальных системах отсчета сохраняется неизменной.

Таким образом, в разных системах отсчета изменяется только поперечная к скорости компонента силы, и, следовательно, меняется направление силы относительно скорости частицы

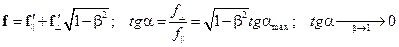
Пусть, например, в лабораторной системе на частицу действует только магнитная сила Лоренца, перпендикулярная скорости частицы: 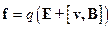. При переходе в сопутствующую систему эта сила должна увеличиться в 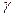раз. Однако в этой системе частица покоится и, следовательно, не может испытывать влияния магнитного поля. Это означает, что в сопутствующей системе появляется электрическое поле 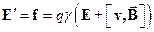и действующая на частицу кулонова сила равна.

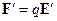Заметим, что если в какой-либо инерциальной системе частица является свободной, т.е. не испытывает силового воздействия, то в любой другой инерциальной системе она также останется свободной, что является необходимым требованием принципа относительности.

Дата добавления: 2014-01-04