Лекция 17. Краткое содержание: Обобщенные координаты механической системы

Краткое содержание: Обобщенные координаты механической системы. Число степеней свободы системы. Обобщенные силы и способы их вычисления. Случай сил, имеющих потенциал. Выражение виртуальных перемещений через вариации обобщенных координат. Условия равновесия системы в обобщенных координатах. Принцип Даламбера для механической системы. Главный вектор и главный момент сил инерции.

Независимые параметры, достаточные для однозначного определения положения рассматриваемой механической системы, называются ее обобщенными координатами .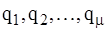

Число независимых параметров m, однозначно определяющих положение системы в пространстве, называется числом ее степеней свободы.

Для каждой из МТ, входящей в СМТ, радиус-вектор можно выразить через обобщенные координаты, которые являются функциями времени:

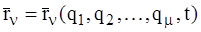n=1,2,…,n (1)

Найдем вариацию радиуса-вектора n-й точки системы:

. (2)

Подставляя эти значения 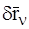в соотношение (1.11) и изменяя порядок суммирования, получим:

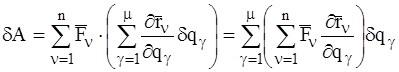. (3)

Введем обозначения:

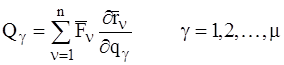. (4)

Тогда выражение для работы сил на виртуальных перемещениях через обобщенные координаты примет вид:

. (5)

Множители Q₁,Q₂,…,Q_m, стоящие в формуле (6) перед вариациями обобщенных координат, называются обобщенными силами, отнесенными к соответствующим обобщенным координатам.

Возможны три способа нахождения обобщенных сил:

· по формуле (4).

· по формуле (5), определив обобщенные силы как коэффициенты при вариациях обобщенных координат в выражении суммы элементарных работ всех сил на виртуальных перемещениях. Учитывая, что вариации обобщенных координат независимы и могут принимать произвольные значения, дадим системе такое виртуальное перемещение, при котором вариации всех обобщенных координат, кроме одной, будут равны нулю, например, 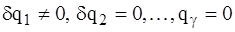, (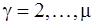). Тогда из соотношения (5) находим 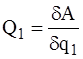, и так далее для всех обобщенных сил.

· когда система находится в потенциальном силовом поле для проекций силы, приложенной к n-й точке, можно записать:

,

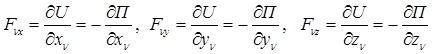где U(x,y,z) – силовая функция, а 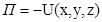– потенциальная энергия. Подставляя эти значения в соотношения (5) и учитывая, что П зависит от обобщенных координат сложным образом, имеем:

.

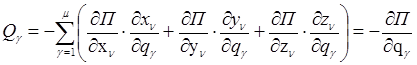Условия равновесия механической системы в обобщенных координатах: Для равновесия СМТ, на которую наложены стационарные, удерживающие и идеальные связи, необходимо и достаточно, чтобы все обобщенные силы равнялись нулю:

.

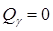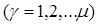
Запишем выражение принципа виртуальных перемещений с учетом соотношения (5):

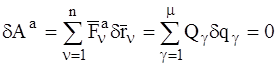. (6)

Доказательство: Так как вариации обобщенных координат 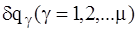независимы и произвольны, то можно сообщить системе такое виртуальное перемещение, при котором вариации всех обобщенных координат, кроме одной, например первой, равны нулю

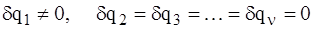(7)

Подставляя (7) в (6) получим 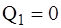и так далее для всех обобщенных сил.

Принцип Даламбера для материальной точки и механической системы.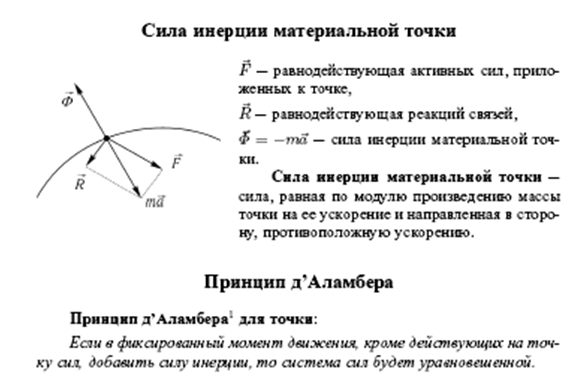

Дата добавления: 2014-01-04