Операции над предикатами

Логические операции над предикатами

Так как предикаты принимают значения на множестве 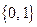, то к ним применимы все логические операции. Пусть Р и Q – предикаты, определенные на предметной области W. Введем определения логических операций над предикатами.

Определение: Отрицанием предиката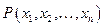называется предикат , определенный на множестве W по правилу:

Определение: Дизъюнкцией предикатов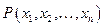и 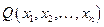называется предикат 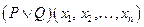определенный на множестве W по правилу:

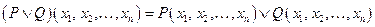
Определение: Конъюнкцией предикатов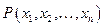и 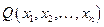называется предикат 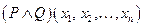определенный на множестве W по правилу:

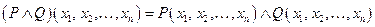
Определение: Импликацией предикатов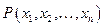и 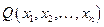называется предикат 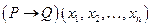определенный на множестве W по правилу:

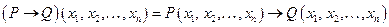
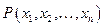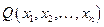Определение: Эквиваленцией предикатови называется предикат определенный на множестве W по правилу:

Определение: Предикаты Р и Q, определенные на предметной области W, называются равносильными (пишут 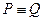), если для любого набора предметных переменных из W:

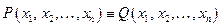
Кванторы

Как было ранее сказано, к предикатам применимы все логические операций, что является обобщением соответствующих операций над 0-местными предикатами (высказываниями) на предикаты произвольной местности.

Однако существуют специфические логические операции логики предикатов, которые относятся не к одной фиксированной ситуации, а ко всему множеству ситуаций.

Определим кванторные операции для одноместных предикатов:

Определение: Пусть 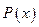– одноместный предикат, определенный на множестве W. Поставим ему в соответствие высказывание 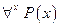(читается «для любого х имеет место 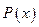»), которое истинно тогда и только тогда, когда 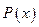– тожественно истинный предикат. Другими словами, высказывание 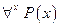означает: «Для любых х без исключений имеет место 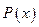». Таким образом, согласно определению:

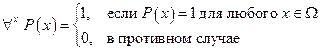
Квантор общности означает конъюнкцию всех значений предикатной функции:

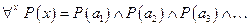
О высказывании 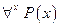говорят, что оно получено из предиката 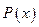навешиванием квантора всеобщности по переменной х.

Определение: Пусть 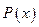– одноместный предикат, определенный на множестве W. Поставим ему в соответствие высказывание 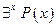(читается «существует х, для которого имеет место 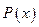»), которое ложно тогда и только тогда, когда 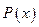– тожественно ложный предикат. Другими словами, высказывание 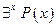означает: «Существует по крайней мере одно значение х, для которого имеет место 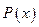». Таким образом, согласно определению:

Квантор существования означает дизъюнкцию всех значений предикатной функции:

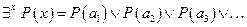
О высказывании 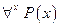говорят, что оно получено из предиката 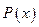навешиванием квантора существования по переменной х.

Таким образом, применение кванторов превращает одноместные предикаты в константы.

Рассмотрим теперь п -местный предикат 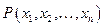на множестве W. Применение квантора общности (существование) по некоторой переменой 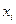позволяет получить предикат местности п -1. Зафиксируем значения переменных , в результате получим одноместный предикат 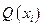. Навесим на предикат 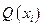по переменной 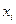квантор всеобщности (существования). Таким образом, набору переменных с помощью квантора всеобщности (существования) поставлено в соответствие высказывания. Другими словами, сопоставление в соответствие любому набору значений переменных вполне определенного высказывание – есть отображение из множества наборов значений переменных во множество высказываний, т.е. является предикатом от переменных . Говорят, что этот предикат был получен из исходного предиката 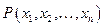навешиванием квантора всеобщности (существования) по переменной 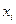и обозначают 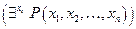. Переменная 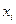, к которой относится квантор, называется связанной, остальные переменные называются свободными.

Пример: Пусть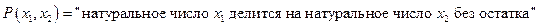

Тогда

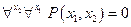
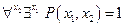
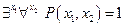
Контрольные вопросы

1. Дайте определение n -местного предиката.

2. Что называют предметной областью предиката?

3. Дайте определение тождественно истинного (ложного) предиката.

4. Что называют логической возможностью предиката?

5. Что называют таблицей истинности предиката? Как ее построить?

6. Перечислите логические операции, применимые к предикатам.

7. Дайте определение отрицания предиката.

8. Дайте определение дизъюнкции предикатов.

9. Дайте определение конъюнкции предикатов.

10. Дайте определение импликации предикатов.

11. Дайте определение эквивалентности предикатов.

12. Дайте определение равносильности предикатов.

13. Какие кванторные операции применимы к предикаты?

14. Сформулируйте определения кванторных операций над предикатами.

Дата добавления: 2014-01-04