Перестановка одноименных кванторов

План

Формулы логики предикатов. Равносильные формулы логики предикатов. Приведенные и нормальные формы в логике предикатов.

Лекция № 18

1. Формулы логики предикатов.

2. Равносильные формулы логики предикатов. Приведенные и нормальные формы в логике предикатов.

§ 1. Формулы логики предикатов

На языке предикатов можно составить гораздо более сложные выражения, чем на языке логики высказываний.

Определим понятие формулы логики предикатов. Алфавит логики предикатов содержит следующие символы:

- символы предметных переменных: ;

- символы предикатов:

- логические символы: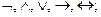

- символы кванторов:

- скобки и запятую:

Слово в алфавите логики предикатов называется формулой, если оно удовлетворяет следующему индуктивному определению (одновременно определяется понятие свободной и связанной переменной формулы):

1. Если – символ предиката, – символы предметных переменных, не обязательно различные, то 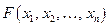- формула. Такая формула называется атомарной. Все предметные переменные атомарных формул свободные, связанных переменных нет.

2. Пусть - формула. Тогда 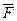тоже формула. Свободные и связанные переменные формулы 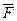– это соответственно свободные и связанные переменные формулы .

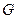3. Пусть и – формулы, причем нет таких предметных переменных, которые были бы связаны в одной формуле и свободны в другой. Тогда

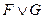
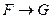
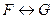
есть формулы, в которых свободные переменные формул и 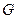остаются свободными, а связанные переменные формул и 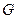остаются связанными.

4. Пусть – формула, содержащая свободную переменную х. Тогда

тоже формулы. Переменная х в них связана. Остальные же переменные, которые в формуле свободны, остаются свободными и в приведенных формулах. Переменные, которые связаны в формуле , остаются связанными и в приведенных формулах. В первой из приведенных формул формула называется областью действия квантора 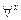, а во второй - областью действия квантора .

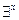5. Слово в алфавите логики предикатов 1 - 5 является формулой только в том случае, если это следует из правил 1 - 4.

Замечание: по определению формулы никакая переменная не может быть одновременно связанной и свободной.

Значение формулы определено только тогда, когда задана какая-то интерпретация входящих в неё символов. Под интерпретацией понимают систему 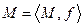, состоящую из непустого множества М и соответствия f, которое сопоставляет каждой формуле определенный предикат. Для заданной интерпретации каждая формула без свободных переменных представляет собой высказывание, которое истинно или ложно, а всякая формула со свободными переменными выражает некоторый предикат на множестве 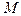, который истинен при одних значениях переменных и ложен при других.

Пример:

Пусть 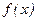- произвольная фиксированная функция, заданная на отрезке .

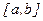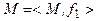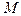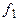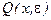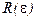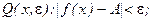
1. Рассмотрим интерпретацию , где - множество действительных чисел; - соответствие, сопоставляющее предикатным символам , и предикаты: Здесь - фиксированный элемент отрезка 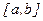. Тогда утверждение о том, что число 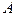предел функци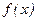и при 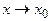записывается формулой .

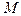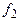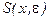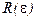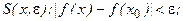
2. Рассмотрим интерпретацию , где - множество действительных чисел; - соответствие, сопоставляющее предикатным символам , и предикаты: Здесь - фиксированный элемент отрезка 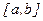. Тогда утверждение о том, что функция 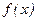непрерывна в точке записывается формулой .

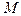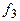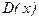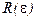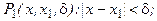
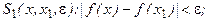
3. Рассмотрим интерпретацию , где - множество действительных чисел; - соответствие, сопоставляющее предикатным символам , , и предикаты: Тогда утверждение о том, что функция 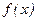непрерывна в на отрезке 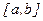записывается формулой

.

§ 2. Равносильность формул логики предикатов

Пусть формулу F и G имеют одно и то же множество свободных переменных.

Формулы F и G являются равносильными в данной интерпретации, если они принимают одинаковые значения на любом наборе свободных переменных, т.е. выражают в данной интерпретации один и тот же предикат.

Формулы F и G являются равносильными на множестве М, если они принимают одинаковые значения во всех интерпретациях, заданных на множестве М.

Формулы F и G являются равносильными (в логике предикатов), если они равносильны на всех множествах (обозначается ).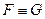

Все соотношения равносильности, имеющие место в логике высказываний, распространяются и на логику предикатов.

Однако помимо равносильностей логики высказываний, в логике предикатов применяются соотношения равносильности, относящиеся к кванторам. К ним относятся:

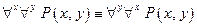
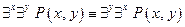
Дата добавления: 2014-01-04