
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Переименование связных переменных
|
|
|
|
Вынос квантора за скобки
Перенос квантора через отрицание





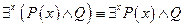

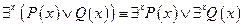
Заменяя связную переменную формулы Р другой переменной, не входящей в эту формулу, в кванторе и всюду в области действия квантора, получим формулу равносильную формуле Р.
Используя указанные равносильносьти формулы логики предикатов можно преобразовывать, упрощать.
Для каждой формулы логики предикатов существует равносильная ей формула, в которой из логических операций имеются лишь инверсия, конъюнкция и дизъюнкция, а знаки отрицаний стоят только над элементарными высказываниями и предикатами. Такая формула называется приведенной формой данного предиката.
Пример: Найти приведенную форму формулы предикатов 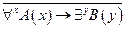 .
.
Решение:
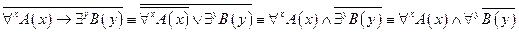
Приведенная формула называется нормальной, если она не содержит символов кванторов или все символы кванторов стоят впереди, т.е. логические символы и символы предикатов стоят в области действия каждого квантора. Нормальная формула называется также нормальной формой данной формулы.
Для преобразования формулы в нормальную форму следует придерживаться следующих шагов:
1. Исключить логические операции эквивалентности и импликации.
2. Используя законы де Моргана преобразовать формулу таким образом, чтобы знак отрицания относился только к элементарным высказываниям.
3. В случае необходимости переименовать связные переменные.
4. Используя равносильности формулы предикатов, преобразовать формулу таким образом, чтобы кванторы находились в начале формулы.
Пример: Найти нормальную форму для формулы 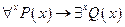 .
.
Решение:

Контрольные вопросы
1. Что называется формулой логики предикатов?
2. Сформулируйте основные правила построения формул.
3. В чем состоит смысл термина «интерпретация» в логике предикатов?
4. Сформулируйте основные правила перехода к новым равносильным формулам.
5. Какая формула называется непротиворечвой, противоречивой, общезначимой?
6. Какая формула называется приведенной? Что такое приведенная форма?
7. Какая формула называется нормальной формой? Сформулируйте алгоритм приведения формулы к нормальной форме.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2457; Нарушение авторских прав?; Мы поможем в написании вашей работы!