Точечная оценка. Доверительные интервалы

Пусть для некоторых изделий с неизвестной функцией распределения наработки до первого отказа определяющим показателем надежности является вероятность отказа изделия Q(t) в течение времени t. В таких условиях прогнозирование вероятности отказа в течение времени, превышающего время испытаний, невозможно. Поэтому выбираем план [N, Б, t], где длительность испытаний Т равна времени эксплуатации изделия t. Устанавливая на испытания N одинаковых изделий и проверяя их работоспособность через время t, определяем число отказавших изделий т(t). Тогда точечной оценкой вероятности отказа является частота Q(t) = m(t)/N.

Согласно закону больших чисел, при увеличении N точечная оценка Q(t) сходится по вероятности к оцениваемой Q(t). Следует, однако, отметить, что при испытаниях надежности далеко не всегда удается установить большое число изделий. Кроме того, для высоконадежных изделий Q(t) обычно очень мало. В этих условиях дисперсия оценки получается неприемлемо большой и точечная оценка становится неудовлетворительной. Поэтому кроме точечной оценки используют доверительные интервалы.

Абсолютно достоверными границами для неизвестной вероятности Q(t) являются 0 и 1. Всякое сужение интервала (0, 1) связано с риском совершить ошибку, состоящую в неверном заключении о том, что Q(t) находится между новыми границами. В зависимости от того, как происходит сужение интервала (0, 1), различают двусторонний и односторонние интервалы.

Двусторонним доверительным интервалом для неизвестной и неслучайной величины вероятности Q(t) называют интервал (Q_н Q_в) со случайными границами, зависящими от исхода статистического эксперимента и такими, что вероятность покрытия этим интервалом неизвестного числа Q(t) не меньше заданной вероятности d, называемой доверительной вероятностью или коэффициентом доверия: P(Q_н£Q£Q_в)

Вероятность противоположного события, то есть того, что Q(t) окажется в интервале (0,Q_н) или (Q_в, 1), называется уровнем значимости Υ и равна 1-d. Уро-

вень значимости можно представитьв виде суммы вероятностей:

Υ=Υ^’+Υ^”=P(0<Q<Q_н)+P(Q_в <Q<1)

Обычно у' и у" выбирают одинаковыми, так что

у ' = у " = у / 2 = (1 - d) / 2.

Односторонними (верхним и нижним) доверительными интервалами называют, соответственно интервалы (0, Q_в) и (Q_н, 1) — такие, что

P(0<Q<Q_в)³d; P(Q_н <Q<1) ³d

Здесь уровень значимости у = 1 - 8 выражает вероятность того, что число Q(t) попадет в интервал (Q_в;1) при верхнем интервале и в интервал (0;Q_н) при нижнем.

Доверительную вероятность нельзя выбирать слишком малой, так как снижается доверие к полученным границам и увеличивается риск сделать неверное заключение. Нельзя выбирать ее и слишком близкой к единице, так как чем ближе d к единице, тем шире границы для неизвестной вероятности. Опыт использования статистических методов показывает, что для практических целей достаточно брать d из диапазона 0,8...0,95. Иногда коэффициент доверия увеличивают до значения 0,98 или 0,99.

Правила вычисления Q_н и Q_в были предложены в начале 30-х годов XX в. английскими статистиками К. Клогшером и Э. Пирсоном. Поскольку испытания различных образцов одного и того же изделия происходят независимо друг от друга, число т отказавших за время t изделий распределено по биномиальному закону с параметрами N и Q, то есть вероятность отказа ровно т изделий из N определяется формулой:

Px=m=C_N^mQ^m(1-Q)^N-m

Вероятность же отказа не более т изделий равна

(1)

Здесь т — вариант, а N и Q — параметры распределения. Функция является ступенчатой функцией т, изменяющейся от нуля до единицы при увеличении т от нуля до N. Если построить семейство распределений у при одном и том же N,

но различных Q и для удобства изображения сгладить ступенчатые функции непрерывными кривыми, то получим семейство зависимостей, приведенное на рис.

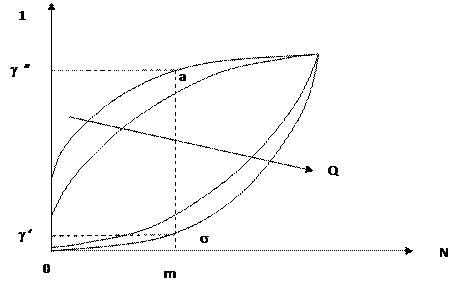В этом семействе параметр Q увеличивается в направлении, указанном стрелкой. Если теперь провести перпендикуляр через точку т, где т — наблюдаемое при испытаниях число отказов, и две горизонтальные прямые на уровне у' и 1 - у", а затем подобрать две кривые семейства, которые проходили бы через точки пересечения а и б, то параметры этих кривых и дают нижнюю и верхнюю доверительные границы с коэффициентом доверия 5 = 1 - у' - у". Два уравнения, составленные для точек а и б, называют уравнениями Клоппера — Пирсона, они могут быть использованы для определения доверительных границ:

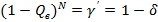
Отсюда

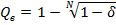
Контрольные вопросы:

1. В чем состоит назначение испытаний на надёжность. Приведите примеры планов испытаний.

2. В чем заключается задача определительных испытаний.

3. Перечислите свойства точечных оценок показателей надёжности

Дата добавления: 2014-01-04